Searching and Binary Search
Searching refers to finding an item in a data structure. The item may or may not actually exist. For example, find a number in an array of integers.
In this article, we'll be focusing on searching linear data structures like arrays, and then in the tree and graph sections, you'll expand on the intuition learned here when applying it to concepts such as binary search trees, depth-first search, and breadth-first search.
Cheat Sheet
| Big O Complexity | |
|---|---|
| search (sorted) | O(log n) |
| search (unsorted) | O(n) |
Searching in Interviews
- Unique binary search examples (ex. rotated array, sparse array, no max size)
- Compare multiple sorted arrays (ex. find the median of two sorted arrays)
- Search a matrix
- Find duplicates
Linear Search
Linear search is a naive and brute force approach to finding an item in a data structure. However, sometimes it is the only option we have. We use linear search when we can make no assumptions about the sort or ordering of data, so items can be randomly dispersed and found at any location.
To perform a linear search, you start at the first spot and iterate through the data one-by-one until you find the item you are looking for. Since we would be required to visit every item in the worst case, it takes O(n) time.
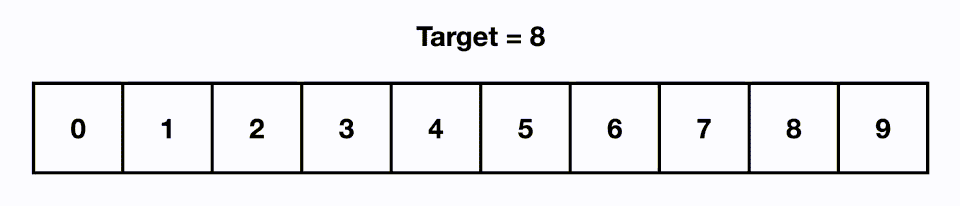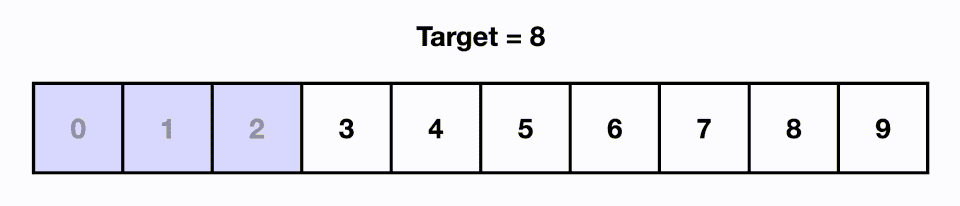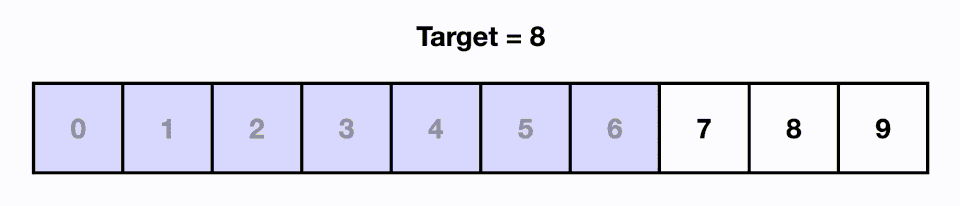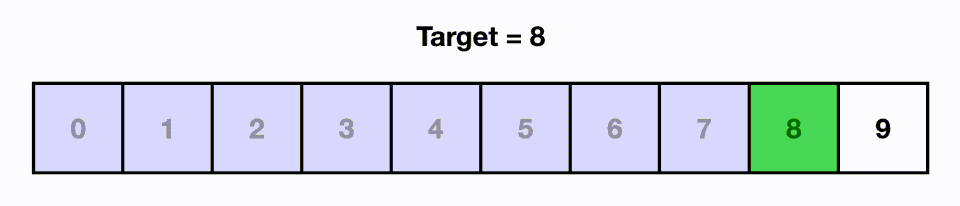
Binary Search
Binary search is basically searching with superpowers and gives us O(log n) time.
The most important constraint for binary search to work: the data must be sorted.
Since our items are ordered from smallest to largest, this additional information allows us to be intelligent about how we look for items. Let's imagine a sorted array. If we picked any random item from the list, let's say the middle item, and we compare it to the target we're looking for. If the target is smaller than the random item we pick, we know it must be to the left since the array is sorted. If the target is larger than the random item we pick, we know it must be to the right.
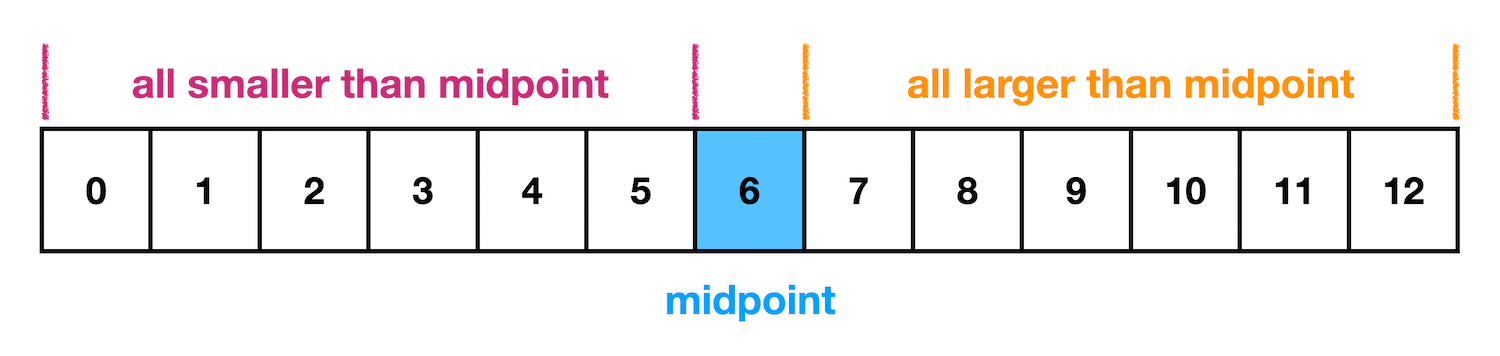
This is the foundation of binary search. We take our input and check the middle item. We can eliminate half of the array if our target is larger or smaller. Then with the remaining items, we repeat this process. We take the middle item of this group and compare it with our target and can eliminate half of the remaining items again. This process is repeated until the target is found.
With every step, we eliminate half of the items in the array. This means we are dividing the amount of data that we need to search by 2 at each step. This is how we get O(log n) time with binary search.
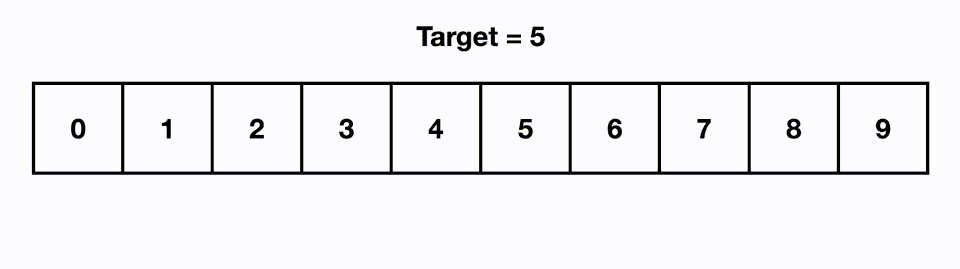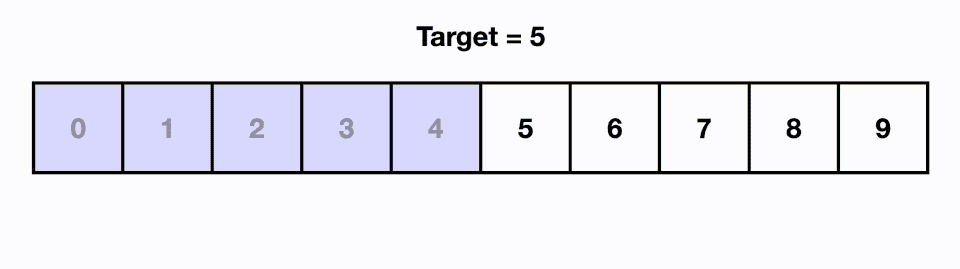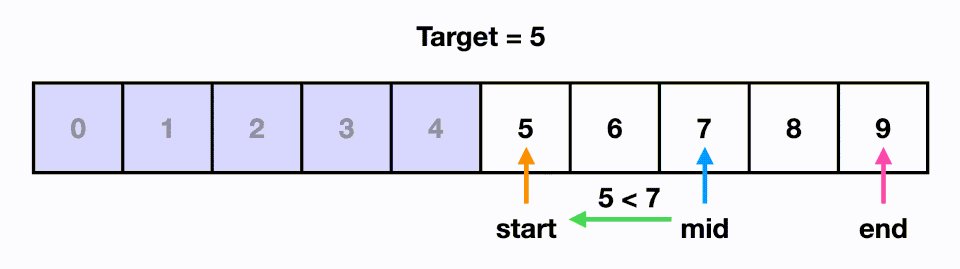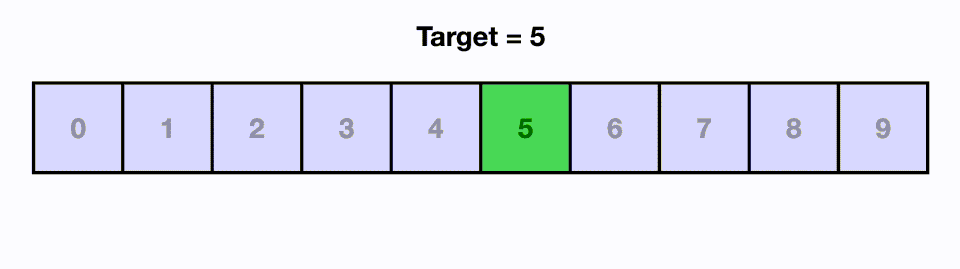
In the above visual, we are able to find our target in 3 moves even though the input size is 8.
If we increase the input size to 16, it would only take 5 moves for binary search to find the last item, but a linear search would need to visit all n items.
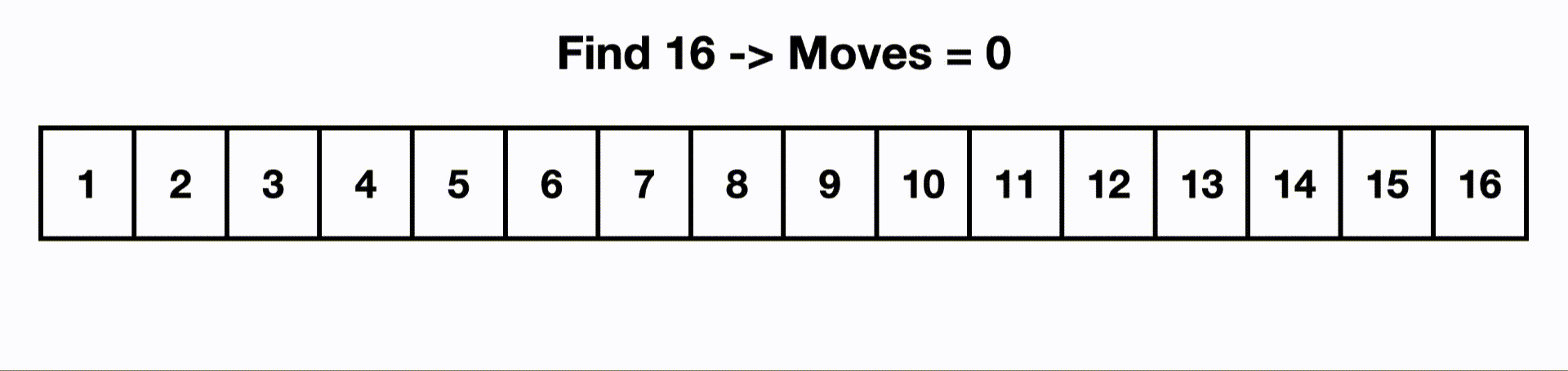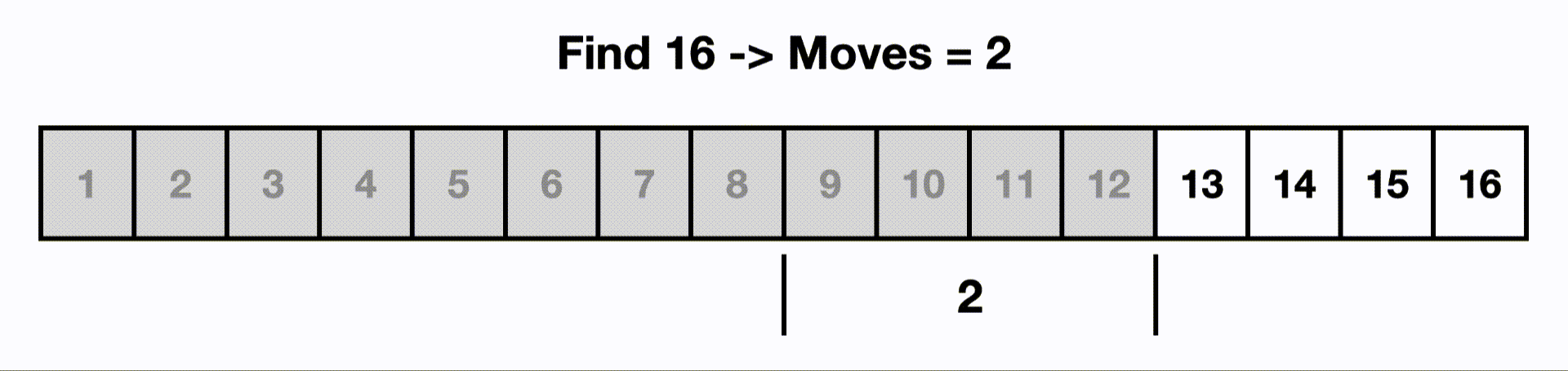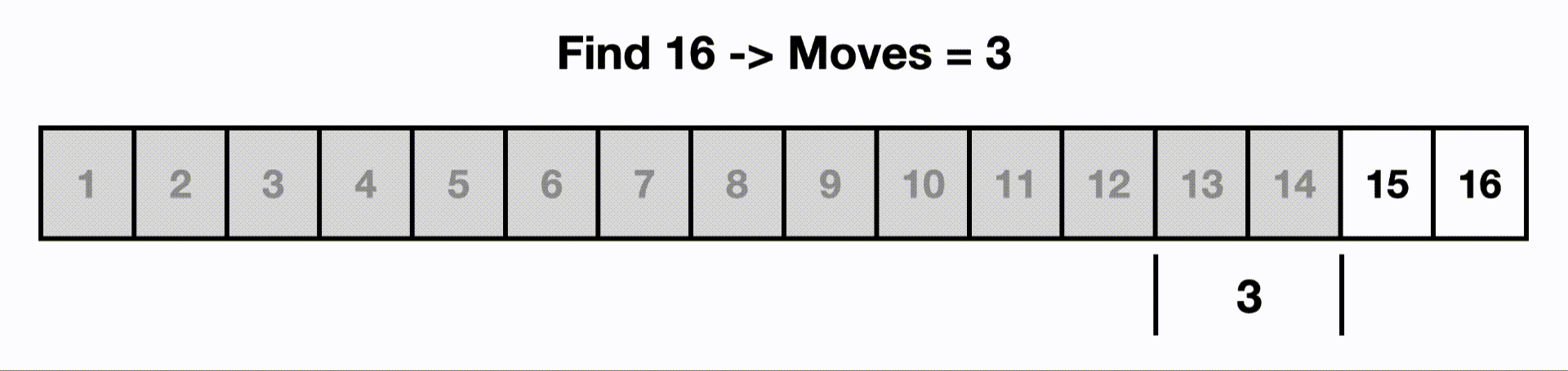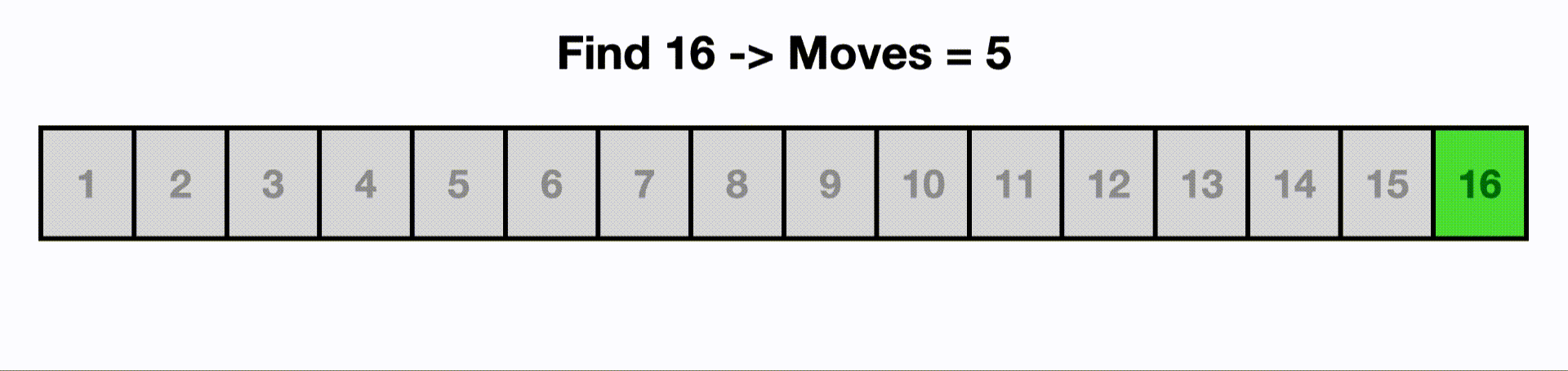
When we compared the time complexity of binary search to linear search in the logarithms article, we saw that operations required for binary search still stays very small for large inputs. For example, at an array of length of 1,048,576 it still only takes 20 operations to find a target in the worst case. Linear search would touch all 1,048,576 items in the worst case.
| input size n | O(n) | O(log n) |
|---|---|---|
| 2 | 2 | 1 |
| 4 | 4 | 2 |
| 8 | 8 | 3 |
| 16 | 16 | 4 |
| ... | ... | ... |
| 1024 | 1024 | 10 |
| 2048 | 2048 | 11 |
| 4096 | 4096 | 12 |
| ... | ... | ... |
| 1048576 | 1048576 | 20 |
Below is the code to implement a binary search iteratively. We track a start and end index for the bounds, which is initially the first and last item to account for the entire array. Then when we determine which half that our target must be in, we either move the lower bound up or the upper bound down to the midpoint which eliminates half the items.
We can implement it iteratively as follows:
Binary search also has a nice recursive solution:
Additional Resources
Binary search can be understood best visually.
If you need some additional practice or want to prove to yourself that it will always converge on the target, you can use the resources below. I also recommend creating some arrays and walking through binary search by hand.