Logarithms and Time Complexity
Logarithms like log(n) can be intimidating at first because they feel so closely connected to math, similar to Big O.
However, you only need to understand a few basic points about them to apply them to your coding interviews.
This article will make logarithms dead simple and show you how to use the concept in interviews.
Simplifying the Math
- Exponents => Multiplication
- Logarithms => Division
If we asked for an exponent 23 = ?, you may recognize that the answer is 8.
It reads as "if we multiplied 2 times itself 3 times, it would equal 8" or 23 = 2 x 2 x 2 = 8.
A logarithm is just the inverse of an exponent.
If we had the equation log2(8) = ?, it would read as "if we divide 8 by 2, how many times would it take for the solution to become 1".
This would be:
log2(8) = 3
8 / 2 / 2 / 2 = 1
- - -
1 2 3I stated logarithms and exponents are inverse operations, just like division and multiplication, but that may not have been immediately obvious.
If you have log2(8) = ?, it's equivalent to saying 2? = 8.
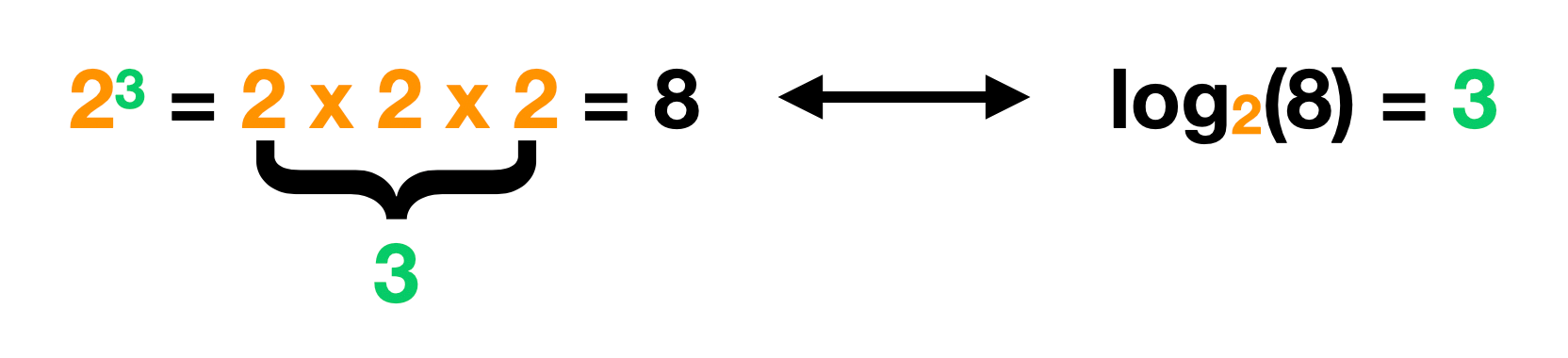
All logarithms need a base, and in the above example we used 2. When we've used the Big O complexity of O(log n), we're typically assuming a base of 2 for O(log2 n). The reason we assume a base of 2 is because the most common operation is to divide by 2 repeatedly each time we perform a step in the iteration over the input. Another way of saying this is that we divide the remaining items in half on each step.
If we change the base though, the logic is still the same.
For example, log10(100) = 2, log10(1000) = 3, log10(10000) = 4, and so on.
So if we had an input size of 16, if we had a O(log n) algorithm, it would touch only ~4 items instead of all 16.
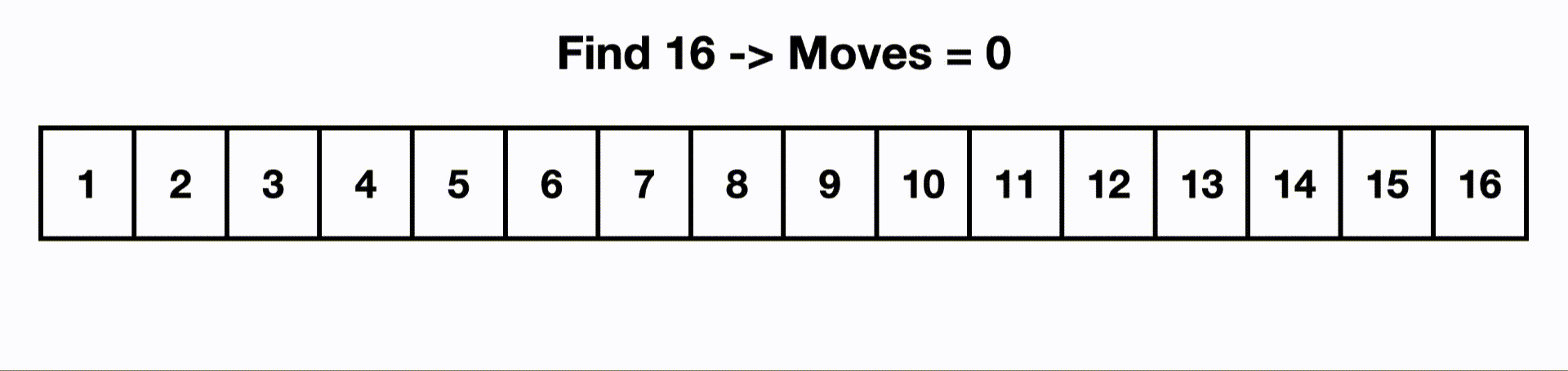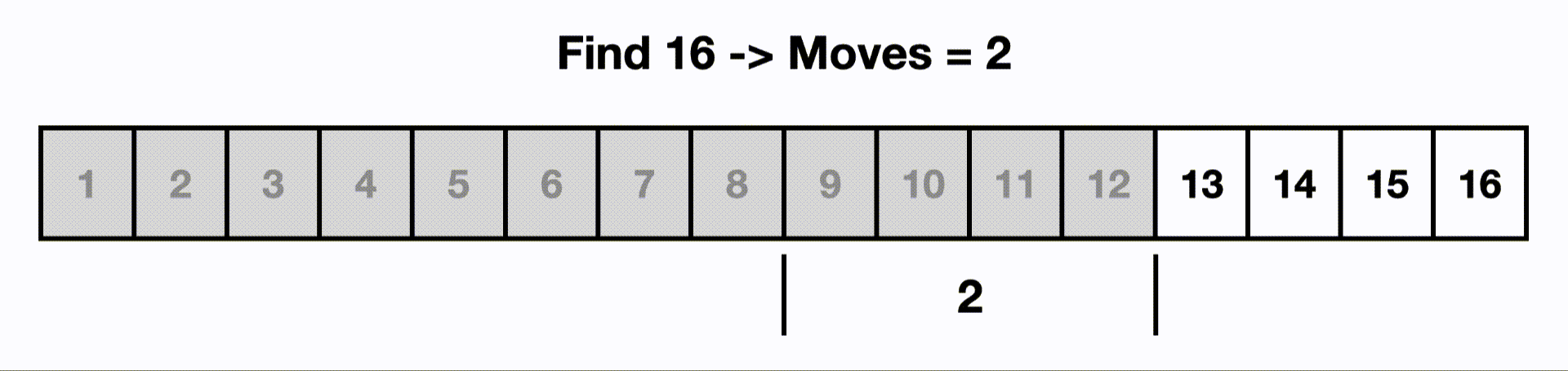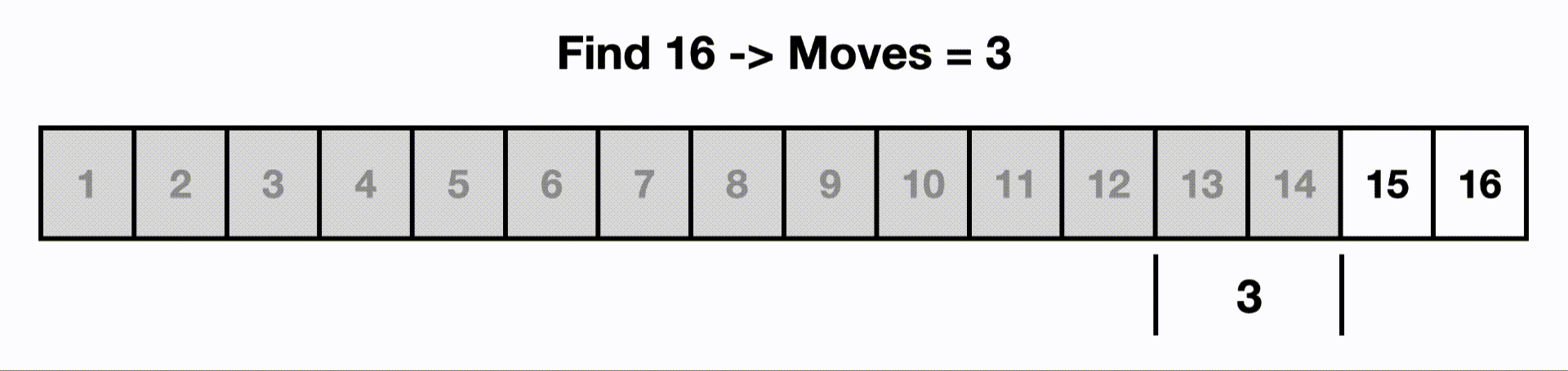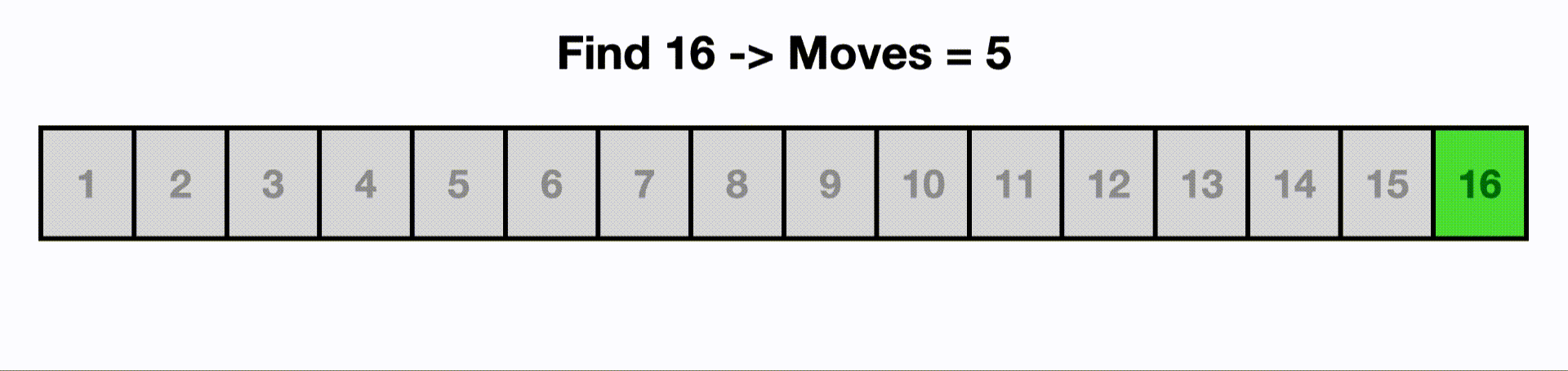
This is an example of a binary search.
Each time we make a move, we cut out half the items because the list is sorted and we know 16 is larger than the current middle item.
If we were to linearly search this, we would start at the beginning and iterate through all n items.
| input size n | O(n) | O(log n) |
|---|---|---|
| 2 | 2 | 1 |
| 4 | 4 | 2 |
| 8 | 8 | 3 |
| 16 | 16 | 4 |
| ... | ... | ... |
| 1024 | 1024 | 10 |
| 2048 | 2048 | 11 |
| 4096 | 4096 | 12 |
| ... | ... | ... |
| 1048576 | 1048576 | 20 |
So you can see that as the number of items in our input increases, the linear O(n) complexity grows at the same rate, but O(log n) increases very slowly even for large input. For example, if you have an input size of 1,048,576, it would only take 20 operations for a O(log n) algorithm. This is because you divide the input by 2 each time, and you only need to do this 20 times for 1,048,576 to reach 1.
In interviews, you most often see logarithmic time in binary search or iterating through a binary search tree. However, as long as you can recognize that your input is being divided on every iteration, this is an indication of O(log n) time.