Trees
A tree is a data structure made up of connected nodes. Each node is simple — it can hold data and can point to child nodes. Trees start at a single root node and branches outward where each child node can have its own children.
By comparison, an array is linear and starts at the 0 index and sequentially lists items up to the final index. With a tree, it starts at the root but each node can have many children which creates multiple paths as opposed to a single linear path. This is why we call a tree a non-linear data structure and is based on hierarchy instead of a sequence.
The most popular implementation of a tree is a binary tree where each node can have at most two children.
Cheat Sheet
| Big O Complexity | |
|---|---|
| lookup | O(n) |
| search | O(n) |
| delete | O(n) |
| space | O(n) |
NOTE: Trees can have many implmentations, and the Big O above is just a reference for the basic tree with no assumed structure. If we instead have a binary search tree, these all become O(log n).
- Represent Hierarchy and PathsTrees are excellent when we need to display data as a hierarchy or need to represent branching decision paths.
- Flexible SizeData does not need to be sequential in memory. We can arbitrarily add/remove items in a tree as long as we have a way to point to the next item.
- No O(1) operationsAll operations require iterating the tree.
Trees in Interviews
- How to iterate through a tree: in-order, pre-order, and post-order traversal
- Binary trees are the most common implementation
- O(log n) search/insert/delete with a binary search tree (BST)
- Create or validate a BST
- Understand the difference between DFS and BFS and when to use each (becomes very important in graphs)
- Understand the depth of a tree
- Edge cases: empty tree, single node, two nodes, skewed tree (a single long path almost like a linked list)
- Use trees to represent hierarchy, model different decisions/paths, maintain sorted data
- Different implementations of trees: binary tree, binary search tree, balanced vs unbalanced, complete binary tree, full binary tree, perfect binary tree
Trees Explained
Trees are something we interact with every day, even if we don't realize it. Some common examples of trees include:
- The file system on your computer
- If someone posts on Reddit, this post (root node) can have many comments, and each of these comments can have replies. These replies can have additional replies, and this all forms a tree that can have an arbitrarily large number of sibling and child nodes below the root.
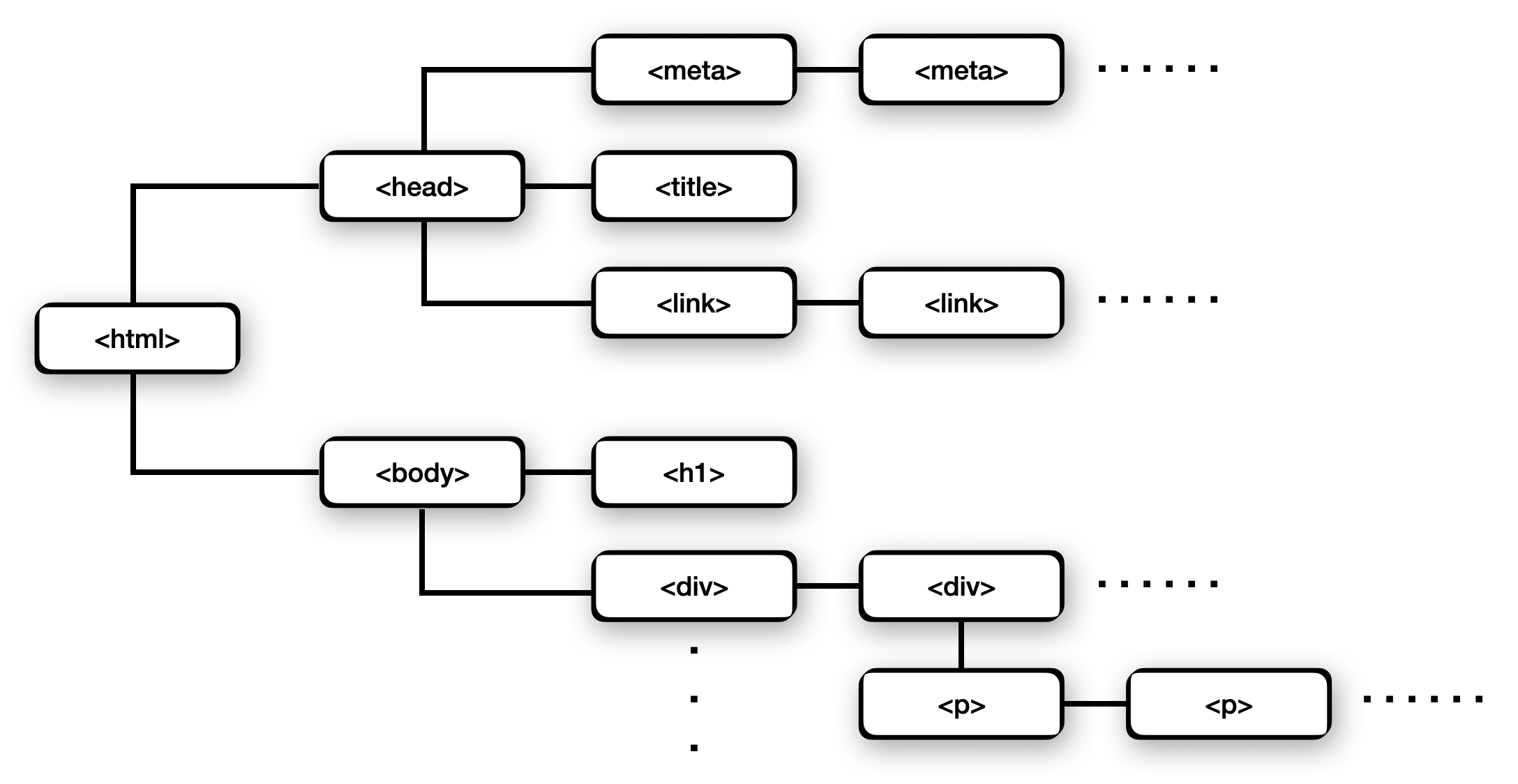
- The DOM is a tree that starts with the
<html>node, has a child<head>and<body>nodes, and these contain thediv,p, and other tags we use to create web pages. - An org chart in a company starts with the CEO at the root, under him are the executives, the managers report to the executives, and the employees report to the managers.
A tree is composed of nodes, and these nodes contain any type of data.
In interviews, this "data" is typically an integer for simplicity but it could take on any data type.
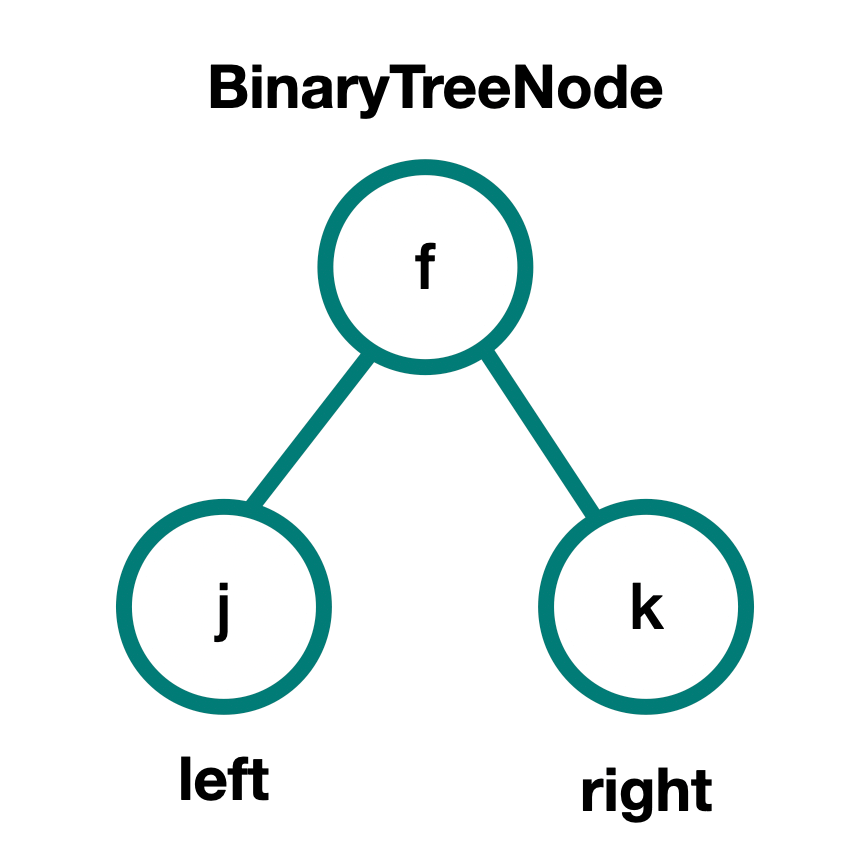
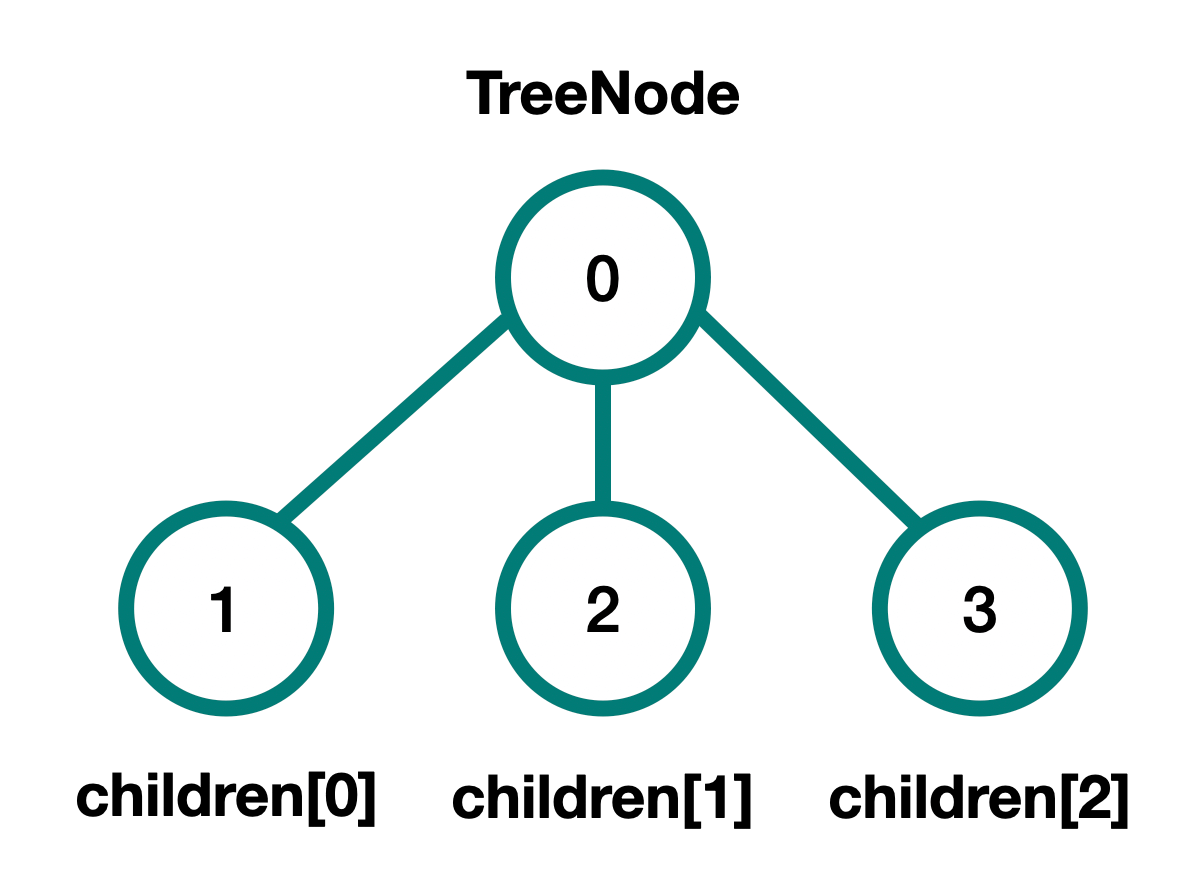
The nodes will also have to their children.
The pointer can either be stored in a variable like a left and right pointer for a binary tree, or for a tree where nodes can have any number of descendants, it can be an array of children pointers.
In interviews, binary trees tend to be the most common tree implementation.
Binary tree node:
Tree node (any number of children):
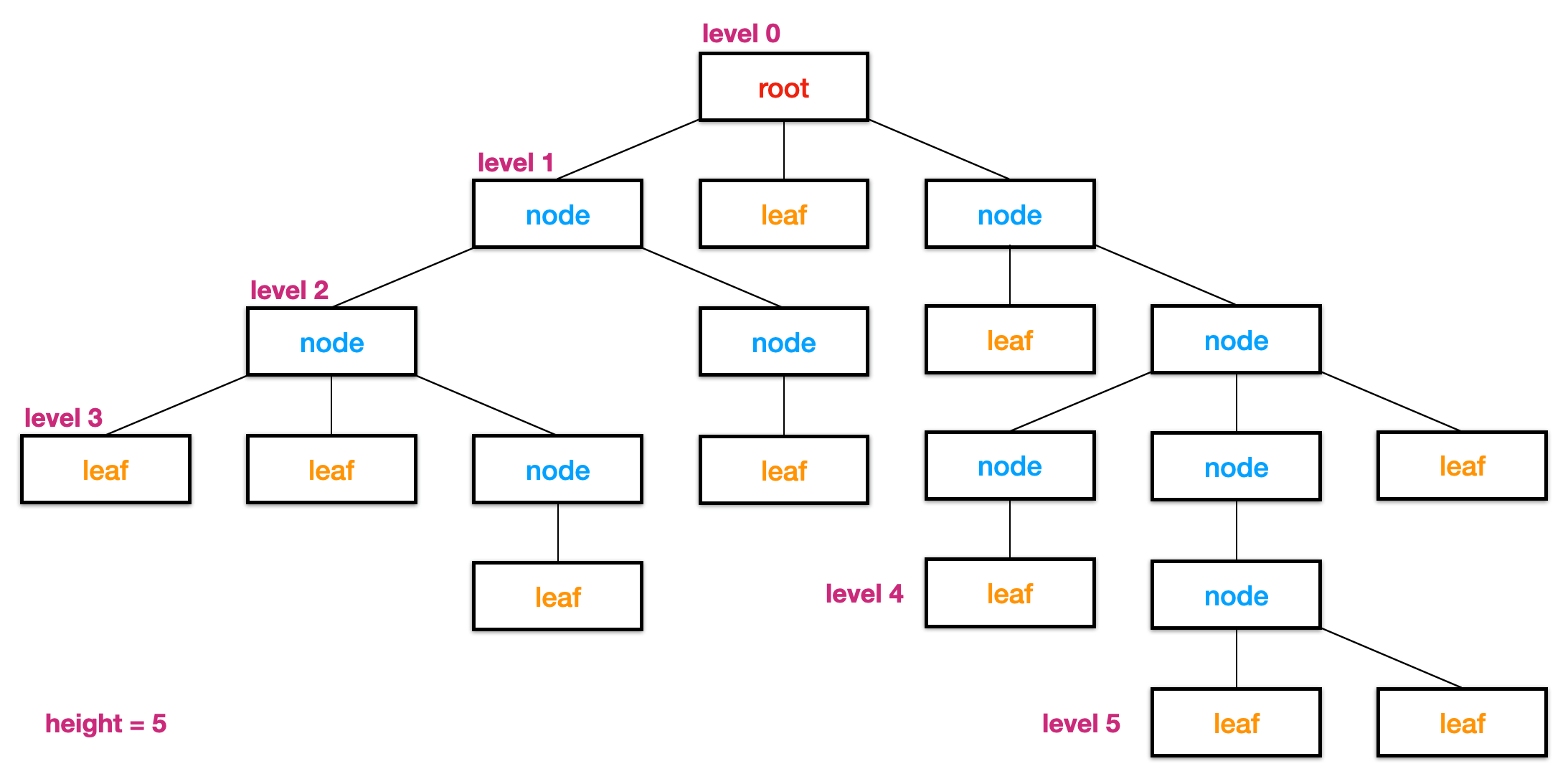
Some common terms used with trees are:
- Node: An item in the tree.
- Edge: A connection between nodes.
- Root node: A single node that is the top-most parent.
- Children: Any node can have children which are just nodes that come directly after it in the tree. We access the children through pointers from the parent.
- Leaf node: A node without children. This indicates we have reached the end of a given path.
- Level: Number of nodes a depth is from the root, where the root node is level 0.
- Height: The largest level (furthest from the root).
To be a categorized as a tree, the data structure must meet the following constraints:
- A tree can only have one root node which has no parent
- Every edge is either directly or indirectly originated from the root
- A node cannot point to itself as a child
- A node can only have one parent
- All nodes must be connected
- A tree can have zero or more nodes
Below are some examples of invalid trees:
The root node points to itself (which also means the root has a parent and is invalid):
Node B has more than one parent:
There is more than one root node and the tree is not connected:
Trees are actually a specialized case of graphs, and these constraints are specifically what makes a graph a tree. So all trees are graphs, but not all graphs are trees.
Types of Trees
We can put additional constraints, the most common being a binary tree where a node can have at most two children. Other classifications include where the nodes are located and how they are arranged.
Tree vs Binary Tree
If any node has more than two children, then we just generally call it a tree. A binary tree means that any given node can have at most two children.
Complete Binary Tree
A complete tree is one where every level must be filled except optionally the last level. If the last level is not full, then it must filled from left to right.
Full Binary Tree
A full binary tree means every node has either zero or two children.
Perfect Binary Tree
A perfect binary tree is both full and complete. All leaf nodes must be on the same level, and that level must be filled.
Binary Tree vs. Binary Search Tree (BST)
The key phrase here is "search".
A binary tree means each node can have at most two children.
A binary search tree means that each node can have at most two children AND all the descendants to the left of any given node are smaller, and all the descendants to the right are larger.
Another way of stating that for any node n is all left children < n < all right children.
This means the tree is ordered.
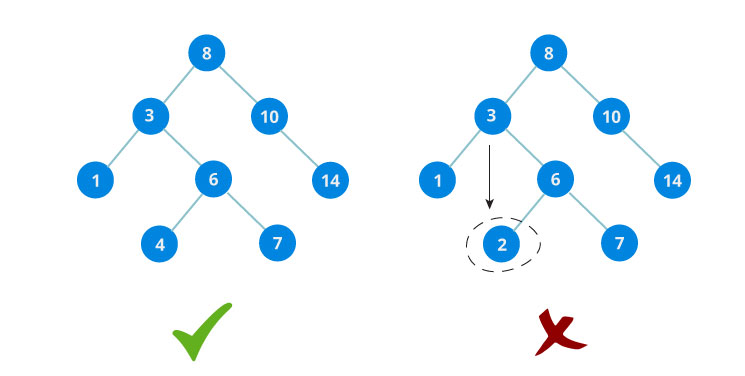
The left tree is a BST, and the right tree is just a normal binary tree but does not qualify as a BST.
A BST can be formed with any of the previous types (ie. balanced, full, perfect), but it also must have the additional constraint of being ordered. So as an example, we could could have a complete binary search tree.
BSTs are a very important implementation and appear the most frequently in interviews. You can learn more about them in their own module.