Binary Search Trees
A binary search tree is a special implementation of a binary tree and is commonly used for tree interview questions. Just like a standard binary tree, each node can have at most two children. Additionally, we call it a "search" tree because it gets fast data access in O(log n) time.
A BST is intentionally constructed in ascending order starting with the left-most leaf node as the smallest value and the right-most leaf as the largest value. This means at any node in the tree, all the children to its left will be smaller, and all the children to its right will be larger. By doing this, we are able to get O(log n) operations.
Cheat Sheet
| Big O Complexity | |
|---|---|
| lookup | O(log n) |
| insert | O(log n) |
| delete | O(log n) |
| search | O(log n) |
| space | O(n) |
- Fast O(log n) for all operationsAssuming we have a balanced tree, all of our operations are fast.
- OrderedWe maintain a BST in ascending sorted order.
- Flexible SizeData does not need to be sequential in memory. We can arbitrarily add/remove items on a tree as long as we have a way to point to the next item.
- Must Maintain BalanceIf the BST isn't balanced, it degrades to O(n) time.
Binary Search Trees in Interviews
- Recognize you can get a O(log n) solution with a BST
- Validate if a binary tree is also a BST
- Build a binary search tree or convert to/from another data structure
- Find the position of an element based on the order
Binary Search Trees Explained
Let's break down the definition of a binary search tree:
Binary Tree: Any node can have at most two children by using a left and right pointer
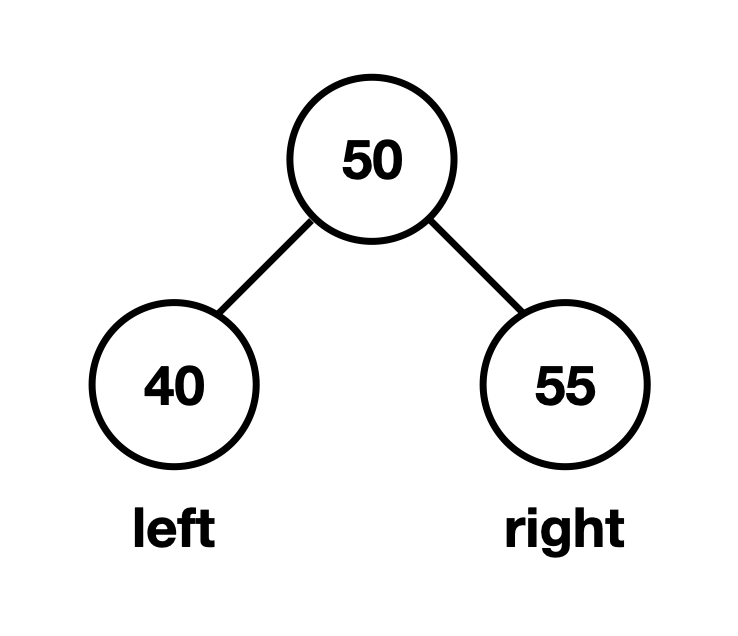
Binary Search: You can perform binary search on the tree because nodes are ordered
So a binary search tree is a sorted binary tree.
This means with a BST, we have ordered data. Looking at any given node, if we follow its left child, all the items will be smaller than the current node. If we follow its right child, all the items will be larger.
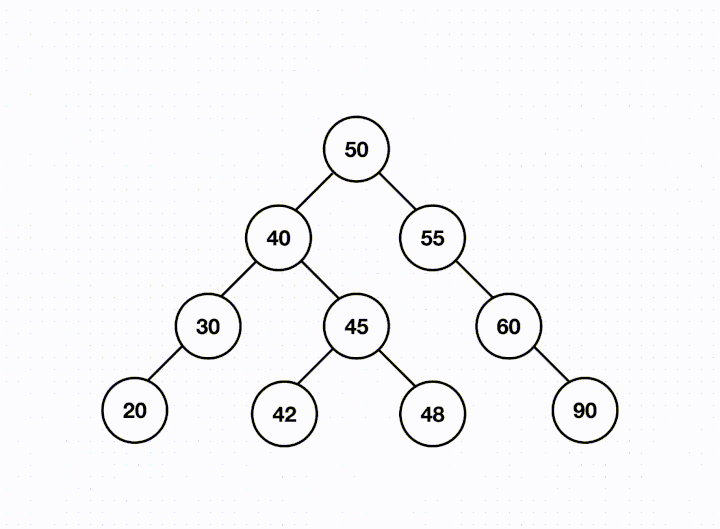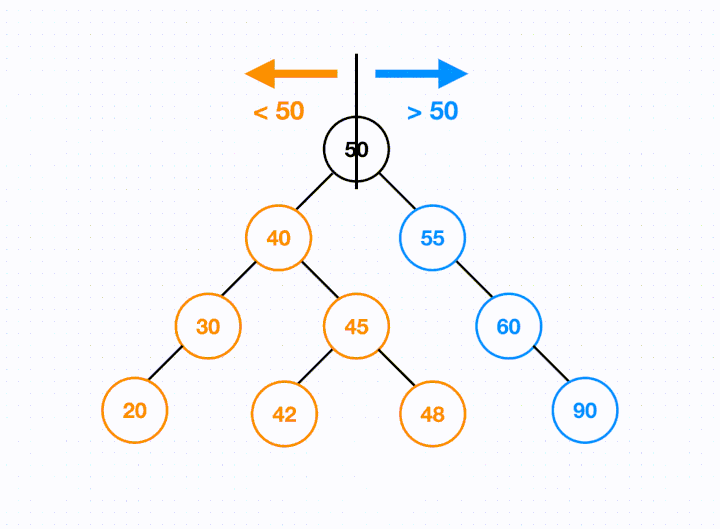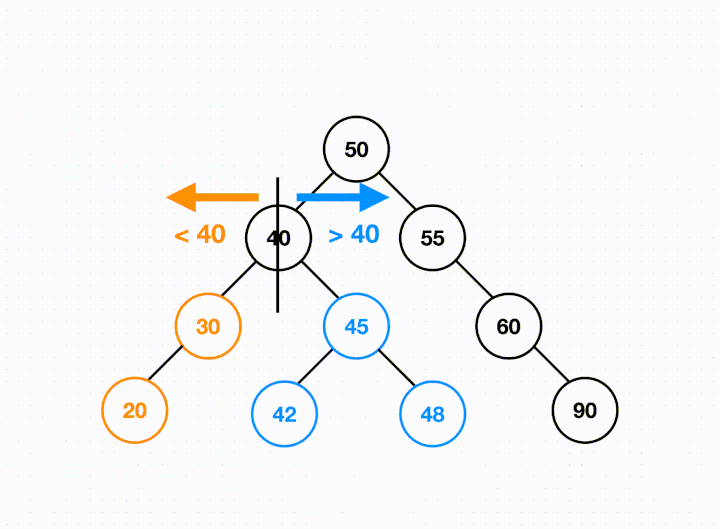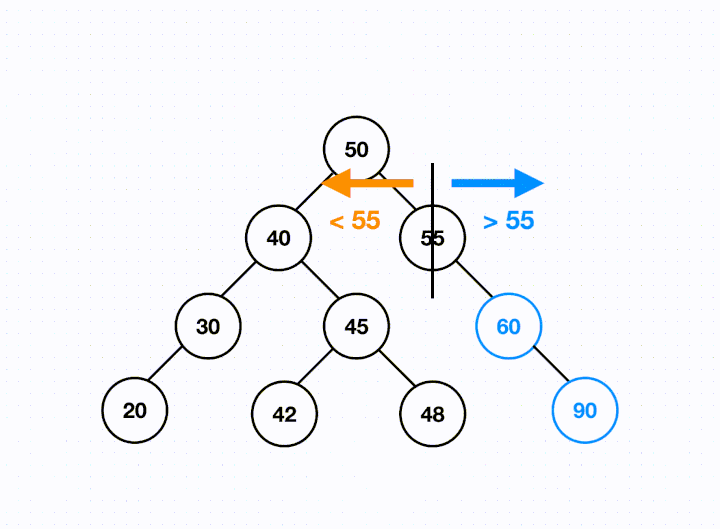
When we see a BST in interviews, it often means two possible things:
- We want to make use of its ordering
- We want to perform operations in O(log n) time
The ordering is what separates a BST from a standard binary tree.
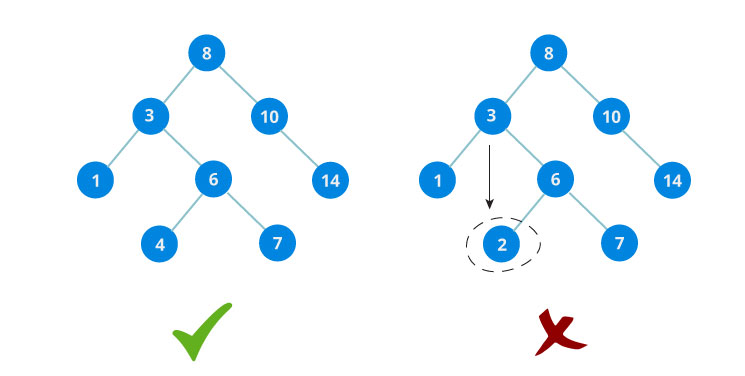
To achieve O(log n) time, the BST much be balanced. There isn't a strict definition of balanced, but it means that every time you traverse to a child, you eliminate approximately half of the remaining nodes. Being able to divide the data by 2 on each step is exactly what it means to be O(log n).
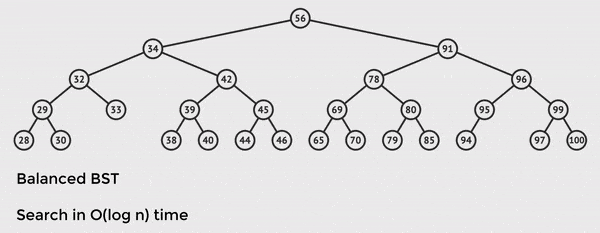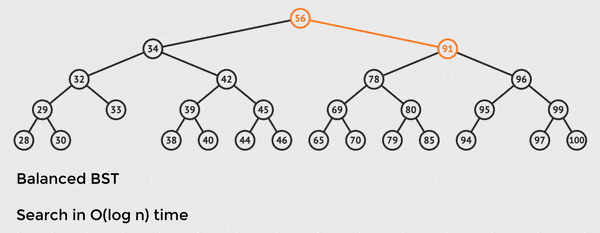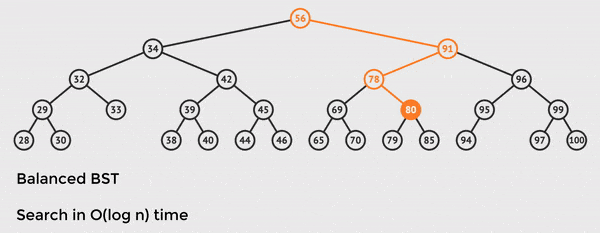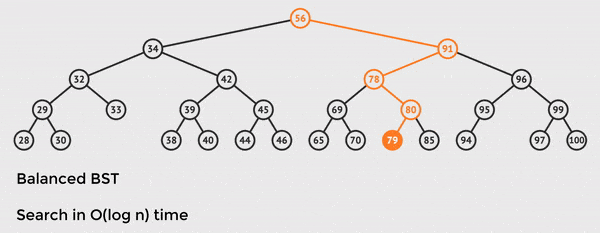
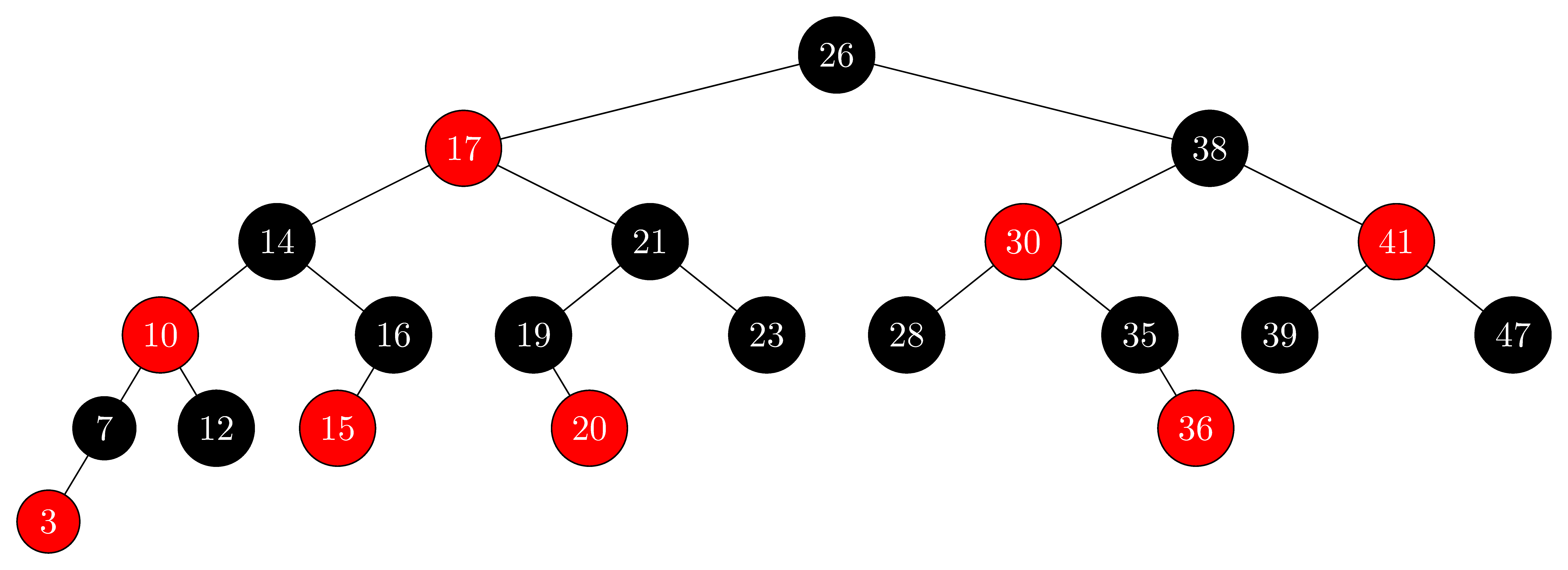
The tree has n = 28 total nodes, but we only need to touch 5 of them to find the value we want.
This is the power of O(log n) time and balanced BST operations.
If our tree is unbalanced, and there is a long path to the final node, it will degrade to O(n) time.
This is because in the worst case where you traverse a long branch of nodes, you must iterate through all ~n items.
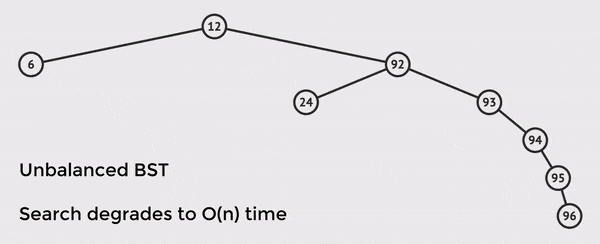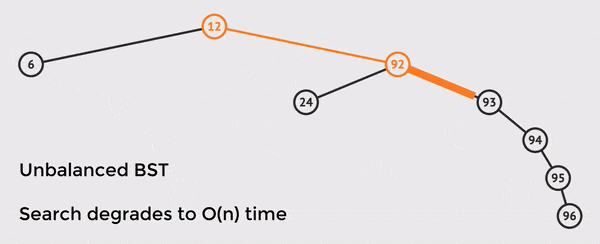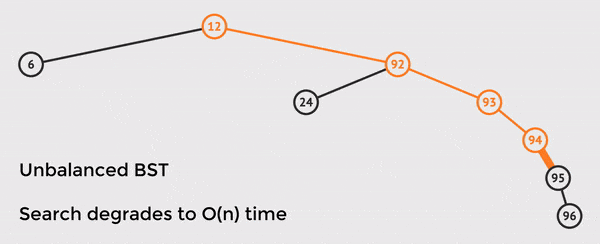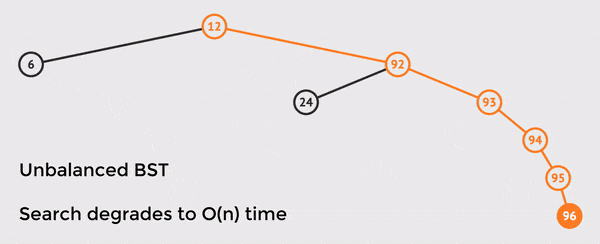
In the example above, we only have n = 8 nodes in the tree, but we must touch 6 nodes in order to find the value.
If we had many more nodes, this would look much worse and is why it's essential to have a balanced tree.
It is rare to need to actually balance a tree in an interview, but you should still be prepared to discuss why being balanced is required to achieve O(log n) time. In production, you will likely use a library to implement balancing, and the two most common are AVL trees and red-black trees. Let's take a quick look at each.
AVL Trees
AVL trees apply a weight to the nodes and will automatically rotate nodes to rebalance if the height of two child subtrees differs by more than one.

Red-Black Trees
Each node in the tree stores an extra data bit in memory which gives a node two possible states that are referred to as red or black. The tree maintains balance by enforcing a specific arrangements of colors and will adjust as needed when new nodes are added.