Dynamic Programming

Dynamic programming is one of the most misunderstood and feared topics for programming interviews. Most explanations use complex terminology and jargon instead of defining the process simply. Here, we'll start from the most basic ideas stated in simple English and build up from that.

Dynamic programming takes time and practice, so work through this lesson, answer the interview questions, and it will eventually click.

As we work through this article, we'll integreate some of the common terminology like subproblem, memoization, and top-down vs. bottom-up, so make sure you have completed those sections first so that this lesson is more clear. You may notice this article looks similar to those previous lessons, and that's because it is. We've already learned all the core concepts for dynamic programming, and this article just ties them together to provide the complete picture.

Dynamic programming is an optimization. After we calculate a piece of a solution, we store it in a data structure so we can use it later instead of performing the calculation again.

Let's re-define dynamic programming so it matches how it's used in interview questions.

"Dynamic programming": Breaking a problem into small increments and solving each as its own step and storing the results for each step in a data structure (often a hash table or array). Once you have all the steps solved, you can combine them to calculate the answer.

Dynamic programming often means calculating ALL the values for ALL steps to reach the desired solution. We store the result of each subproblem so it only needs to be calculated once, which is the key to dynamic programming. While it might sound inefficient to use all the values at all the steps, oftentimes it is the only way. The optimization is that we store the results of each step so we only perform each calculation once when we have the overlapping subproblems.

The keys to dynamic programming:

1. There are subproblems: we can solve the same problem repeatedly with different input values and combine them to calculate the solution
2. The subproblems are overlapping: the algorithm requires the solution from a subproblem using the same input value multiple times
3. We can memoize the results of overlapping subproblems to remove duplicate work: after calculating the solution to a subproblem with a given input, we store its result in a data structure (often a hash table or array)

With dynamic programming, each subproblem is a decision. At each point, we consider the current value and the solutions to the subproblems we previously calculated. Then we make the best choice to solve the current subproblem given the data available to get the local solution at each step. Once we have solved the problem at each step, we will have calculated our overall solution.

The key to dynamic programming is learning to think in subproblems, and this comes with practice. Don't memorize tables or recursive trees. Learn to think about solving the problem in steps using the same logic at each increment but with different input values. Then just store the answer in a data structure so you don't have to repeat the calculations again. You look backward in the data structure and utilize previously calculated solutions.

Dynamic Programming Example

Let's take calculating a Fibonacci number as an example for dynamic programming. Any given Fibonacci number is defined as the sum of the two numbers that come before it in the sequence. So the 100th Fibonacci number is the 99th + 98th fib(100) = fib(99) + fib(98). But to find the 99th and 98th, we must find the two numbers before each of those.

So to find the value of the 100th Fibonacci number, we find the value of all 99 Fibonacci numbers before it. Each calculation introduces overlapping subproblems because each number is used multiple times to calculate any given Fibonacci number. Finding the value of these 99 numbers step-by-step and using memoization to remove the duplicate calculations is exactly how dynamic programming works.

The key is storing the result calculated in each step. fib(100) = fib(99) + fib(98), but fib(99) = fib(98) + fib(97). So both fib(100) and fib(99) each need fib(98), so we only need to calculate fib(98) once and then we can reuse its value when needed. We do this for all values that we calculate in the Fibonacci sequence so we solve each step only once.

Dynamic programming can be used in either top-down or bottom-up algorithms. In either case, we use a data structure (often a hash table or array) to store the results as we build our solution.

With top-down, we store the result of a recursive function call for a given input. The key in the hash table is the function input, and the value for the key in the hash table is the result returned from the recursive function for that input.

With bottom-up, we start with the smallest value and build up our hash table as we continue to solve each step. The bottom-up approach uses previously calculated values stored in the hash table to determine the current value. This repeats until you reach the solution.

Dynamic programming is only an optimization when you have overlapping subproblems and storing the value for each step removes duplicate work. If there are no overlapping subproblems, then storing the result for each step is likely unnecessary (and could incur unneeded space complexity) because you will only be required to calcualte that step once to find the solution. You can use a standard recursive or iterative solution without dynamic programming to solve the question.

Let's consider Fibonacci with a top-down and bottom-up dynamic programming solution. It is important to note that the approach and way we think about it doesn't change — we break the question into subproblems and solve each with different input values. All that changes is the implementation in either starting at the smallest value and working up, or starting at the largest value and working down.

Top-Down Fibonacci Dynamic Programming

Many developers find dynamic programming to be easier to grasp by using recursion since we more explicitly declare the subproblems. We go top-down by starting with the desired result and solving subproblems recursively by changing the input until we reach the base case. Once we have the base case, we start building the solution up until we reach our initial function call.

For example, with the Fibonacci, we calculate it recursively as the following:

So if we're specifically talking about dynamic programming implemented recursively, we could define it as: solving a problem recursively and storing the results of recursive calls in a data structure so you don't call a function again with the same parameters more than once. With a top-down approach, we can simply think of dynamic programming as just an optimization on top of recursion by using memoization.

If we have overlapping subproblems, all we're really saying is that different recursive calls need a result from the same recursive function. For example, think of calculating the 5th Fibonacci number.

fib(7) = fib(6)   +   fib(5)
        /      \     /      \
       f(5) + f(4)  f(4) + f(3)

To calculate fib(7) we need fib(6) and fib(5), but to calculate fib(6) we also need fib(5). In addition, both fib(6) and fib(5) need the result from fib(4) to calculate their values. These are overlapping subproblems, and we use memoization to store the result of function calls so they don't have to be recursively calculated each time.

Fibonacci without memoization requires ~O(2ⁿ) time complexity. With n = 7, we have over 40 operations.

Credit: VisuAlgo

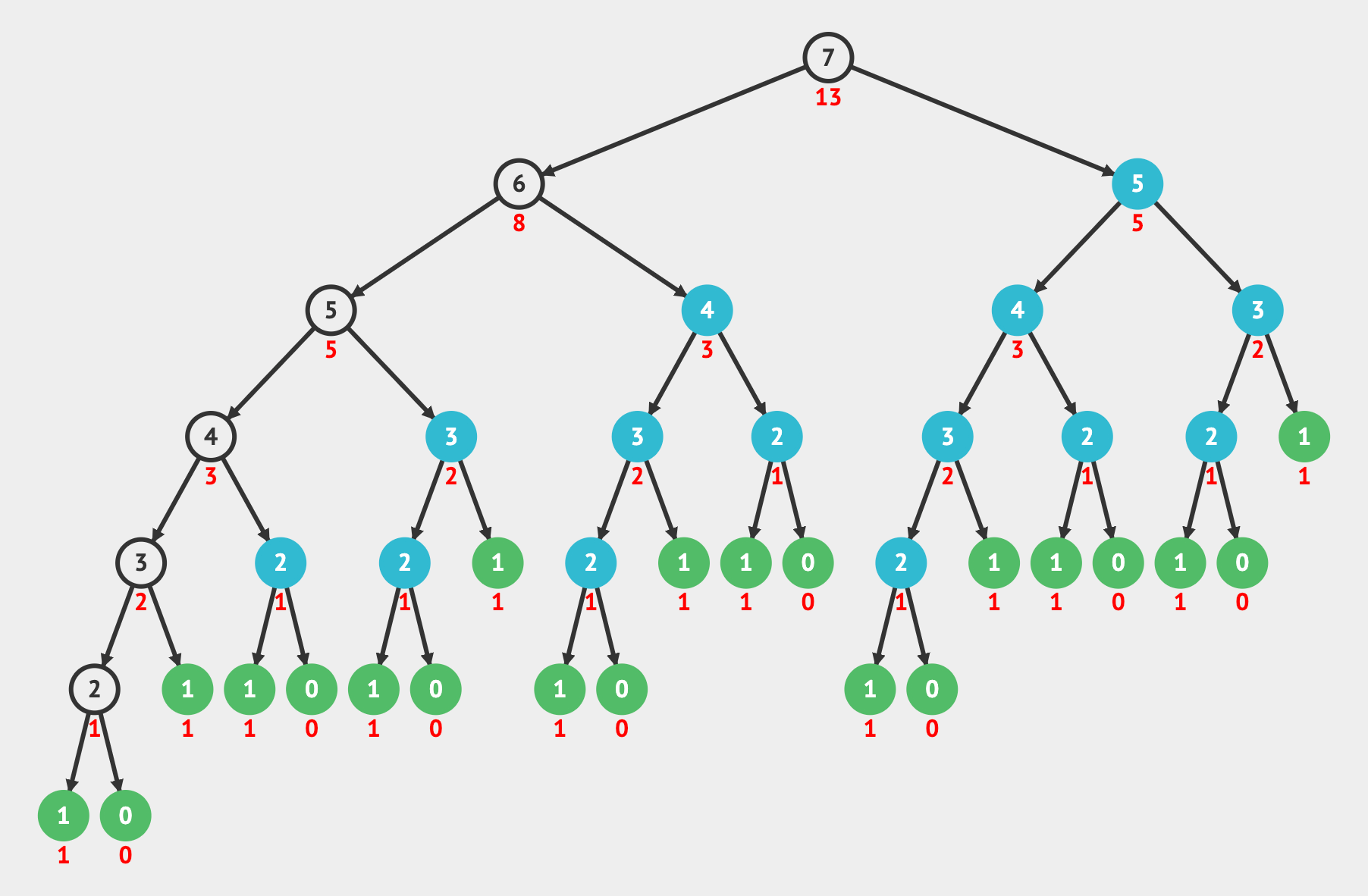
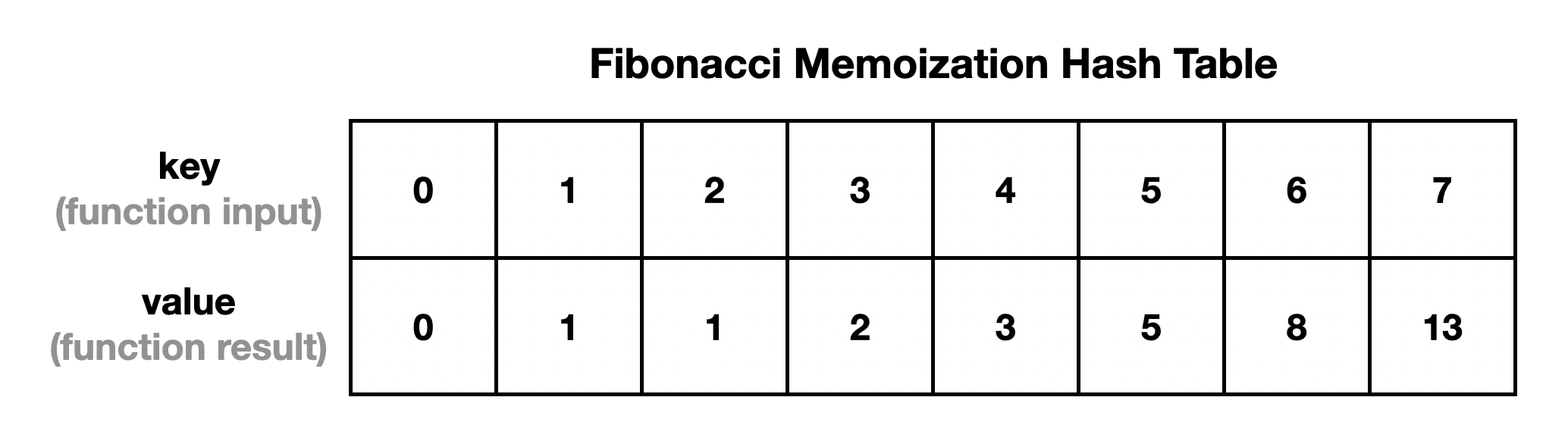
With dynamic programming, we memoize the results and build up a table that we can read from to get previously calculated values instead of recalculating them and introducing duplicate work. So as we calculate a value in the Fibonacci sequence, we can store its result in a hash table:

Or in code:

When we read the memoized results from the hash table, it allows us to reduce the Fibonacci calculation to O(n) time by adding O(n) space. We remove the duplicate work and only perform the calculations shown in the image below. The blue nodes are when we read from the memoization table for a value that was previously calculated.

Credit: VisuAlgo

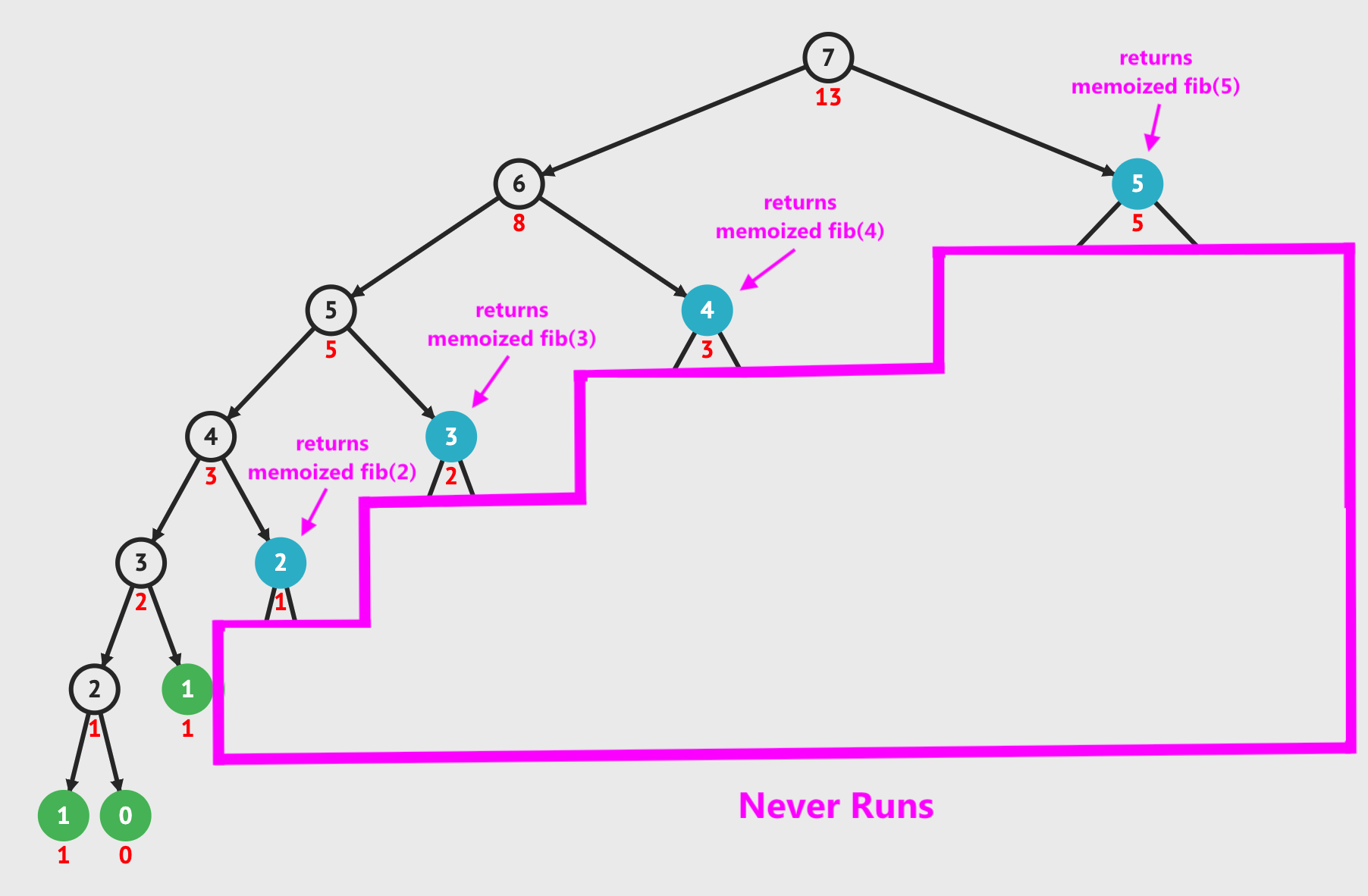
That's really all there is to it. If you can feel comfortable with recursive thinking and understand how to store data in another data structure, you can tackle almost any dynamic programming question. Not only that, they can even become very easy for you.

Bottom-Up Fibonacci Dynamic Programming

Any question that can be solved recursively can also be solved iteratively. Recursion is just a simple way to think about how to break a problem into smaller subproblems. Solving a problem recursively is called a top-down approach and solving a problem iteratively is called a bottom-up approach.

With bottom-up Fibonacci, we start at the smallest values we know and build up our hash table again and calculate the current value using the previous two values until we reach our solution. Again, we're using memoization and solving subproblems to get our answer.

At each iteration of the loop, we are solving a subproblem. We calculate the current Fibonacci number by looking backward in the memoization data structure and use the result from previous subproblems where we calculated prior Fibonacci numbers.

Using a data structure is actually not required to calculate a solution for bottom-up Fibonacci since we can just store the previous two Fibonacci numbers in variables. However, very often in dynamic programming bottom-up solutions, you will need to construct a full table like this to solve your subproblems efficiently.

Dynamic Programming in Interviews

Enough with the Fibonacci, am I right? Let's take a look at some common examples of dynamic programming and classic DP questions.

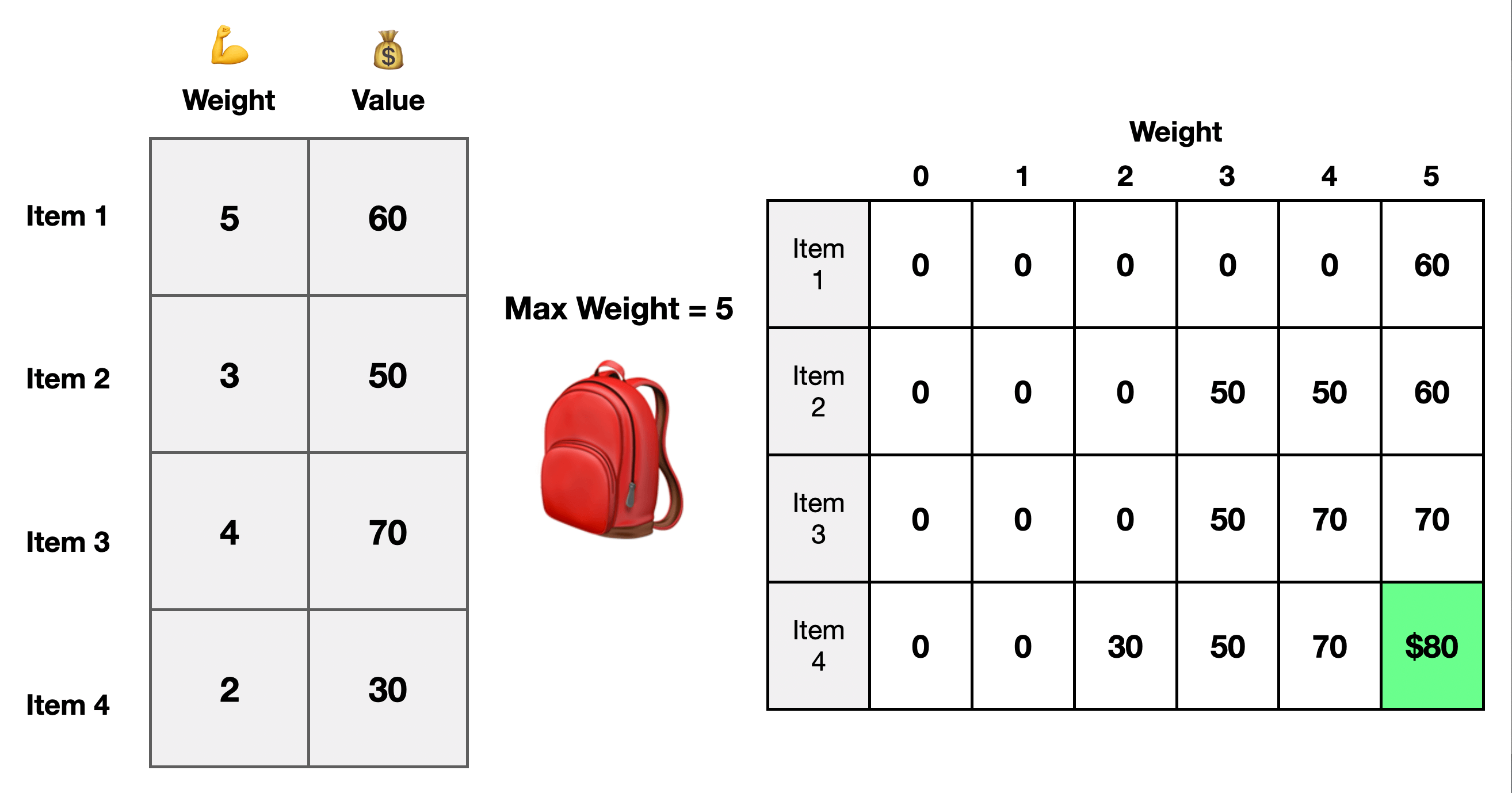
Knapsack Problem

The knapsack problem is a classic dynamic programming interview question. We have a list of items, and each item has a weight and value. You want to find the largest value from any combination of items while keeping the weight below a certain threshold.

You iterate through all the items. Then go from 0 to the max weight for each item and determine which item is best to keep at each point. So we have subproblems where try each item at each weight. We memoize the solution to each subproblem, and then as we try the new item combinations, we use the previously calculated optimal solutions and test it against the current item and keep the combination that provides maximum value while staying under the allowed weight.

With dynamic programming, each point is a decision. We make the optimal choice based on the current input and previously calculated solutions to subproblems. Here we decide at each step if we should keep the current item or use a previous item to produce the maximum combined item value.

This allows us to build up our solution, and once we have tried all the item combinations at all the weights, we will have solved the problem.

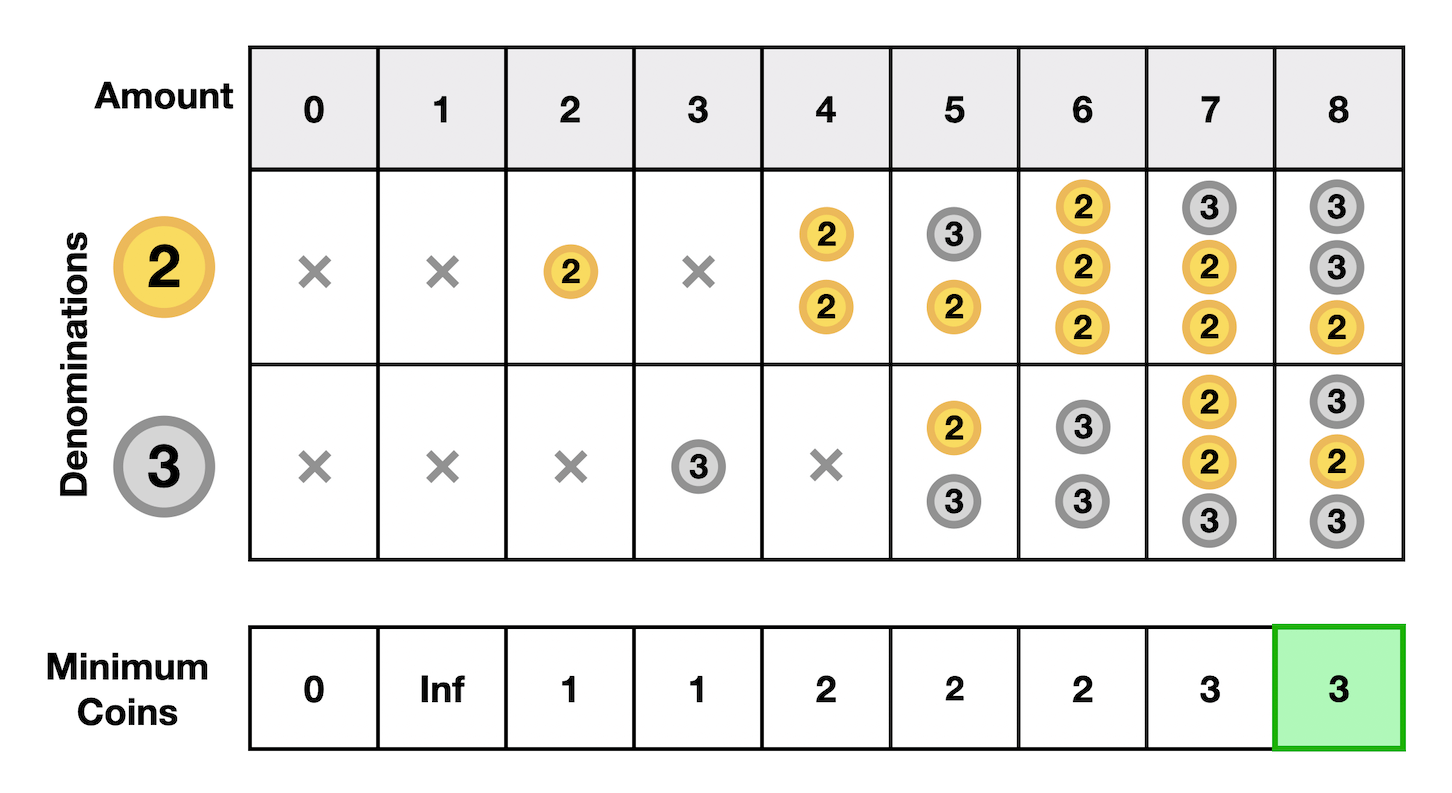
Coin Change

There are a few ways to ask this question, but they all revolve around combining various change denominations. In this course, we have a similar question where you find the minimum number of coins required to calculate a target value from available denominations.

We solve this by starting at zero and finding the minimum coins to reach every value up to the desired target value. We try every denomination at every value. At each point, we keep the minimum number of coins required to reach the current value, and we determine this by using the minimum coins used to reach prior spots.

Each step is a decision where we choose the denomination that will allow us to reach each current value with the fewest coins. By finding the minimum coins to reach each value from 0 up to the target locally in each subproblem, we will have solved the problem globally once we reach the end.

What Do They Have in Common?

Both of these examples follow the same pattern we see in dynamic programming. They solve subproblems, which means at each point, we solve the problem locally for a given input and look at back previously calculated optimal subproblem solutions to make the best choice at the current step. We use memoization to build up the answers to the subproblems. Once we reach the end, we will have solved the problem globally and have the answer.

Summary

Dynamic programming is an optimization, and we use it when we have overlapping subproblems. We use a data structure (often a hash table or array) to memoize the result of subproblems so we only perform the calculation for each input value only once.

Each subproblem is just its own problem. We find the best solution for this step based on the available information we have. Each subproblem is a decision, and we make the choice that will solve it optimally at this point. We store this value which will be used later to find the answer to future subproblems. After solving each problem locally, once we reach the end, we have solved the problem globally and will have our answer.

If there are subproblems but they aren't overlapping (ie. you need to calculate the solution to a subproblem only once), then dynamic programming/memoization is not an improvement.

To restate the introduction, the keys to dynamic programming:

1. There are subproblems: we can solve the same problem repeatedly with different input values and combine them to calculate the solution
2. The subproblems are overlapping: the algorithm requires the solution from a subproblem using the same input value multiple times
3. We can memoize the results of overlapping subproblems to remove duplicate work: after calculating the solution to a subproblem with a given input, we store its result in a data structure (often a hash table or array)