Subproblems and Overlapping Subproblems
From my experience, resources that teach dynamic programming gloss over subproblems and assume you already know them (or perhaps don't know how to teach it). You usually see a phrase like, "If you recognize overlapping subproblems, it's a great opportunity for dynamic programming." However, without understanding what a subproblem is, you can't feel confident implementing dynamic programming or possibly even recursion.
Subproblems
I'll first define what a subproblem is, and then we'll walk through it step-by-step. Solving subproblems means we take a function and call it multiple times with different input values. We start with the smallest value and build up to the largest (bottom-up) or recursively decrease the input from the largest value down to the smallest (top-down) until we reach the base. Then we combine the results of all the function calls to calculate the solution.
We previously saw that we could recursively solve for the factorial for any number n!.
It took the following form (ignoring the base case for now):
factorial(n) = n * factorial(n - 1)
What we did was recognize a subproblem.
To find the factorial of any number n, you can multiply n * (n - 1)!.
And then this repeated because (n - 1)! = (n - 1) * (n - 2)!.
So you need the number before the current n to find the solution, but then you need the number before n - 1 to solve for that number.
This logic continues until you reach the base case.
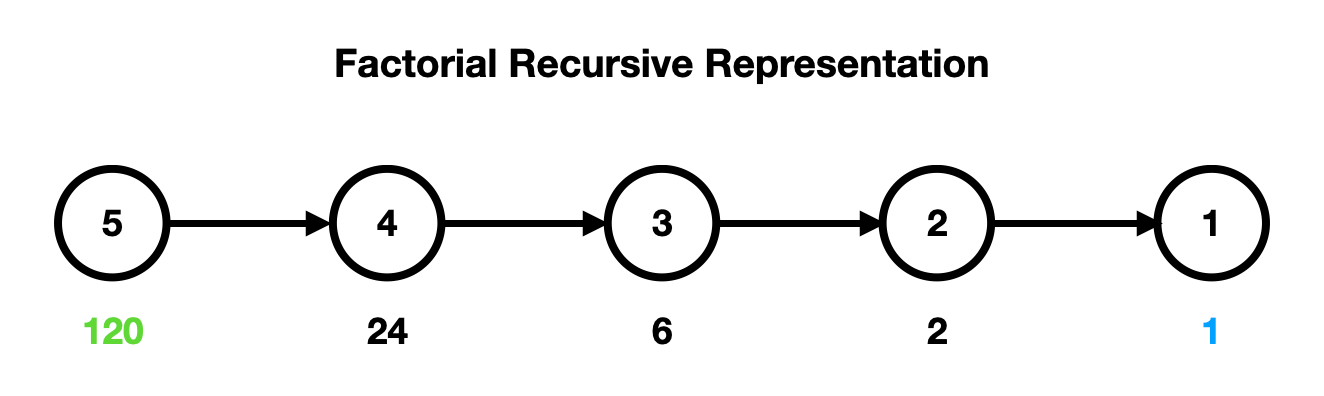
The image below is a visual for factorial recursion.
Each of the steps where you change the input the value to factorial is solving a different subproblem.
You combine them by multiplying each current number by the result of the subproblem before it to eventually calculate 4!.

So to explicitly state what's happening, we can say 4! = 4 * 3! which is 4! = 4 * 3 * 2! which is 4! = 4 * 3 * 2 * 1.
You repeat the same logic over and over from the base case up to the n! you're looking for.
The only thing that changes is the input value at each step.
The solution for each step is returned to the function call that invoked it, and this function can then use this result to calculate the solution to its own subproblem.
By building up the results to each subproblem, we can eventually calculate n! of the original function invocation.
If we wanted to calculate factorial(1000), we don't need to actually know what factorial(999) and factorial(998) are.
By specifying the correct base case and recursive case, the result of all the preceding subproblems will produce the solution we need.
Overlapping Subproblems
Up to this point in this article, we haven't discussed overlapping subproblems, because there aren't any with the factorial function. They are all subproblems called with unique values.
For overlapping subproblems to occur, our function will be called with the same input value multiple times. This most often happens when we have more than one recursive call in a recursive function.
For example, the logic for finding a Fibonacci number is the following:
fib(n) = fib(n - 1) + fib(n - 2)
We have subproblems where we can calculate the Fibonacci number for any value n.
So then to calculate any given Fibonacci number, we just need the results of the Fibonacci numbers before it.
We require two recursive function calls to calculate a number: fib(n - 1) and fib(n - 2).
So if we wanted fib(100) = fib(99) + fib(98),
both fib(99) and fib(98) would separately generate all the numbers fib(97) to fib(1)
because fib(99) = fib(98) + fib(97) and fib(98) = fib(97) + fib(96).
Each step generates many more function calls, and we call fib with repeated input values many times.
This branches outward with each nested step continuing to do the same thing.
If we look at fib(7), we can see the repeated calculations:
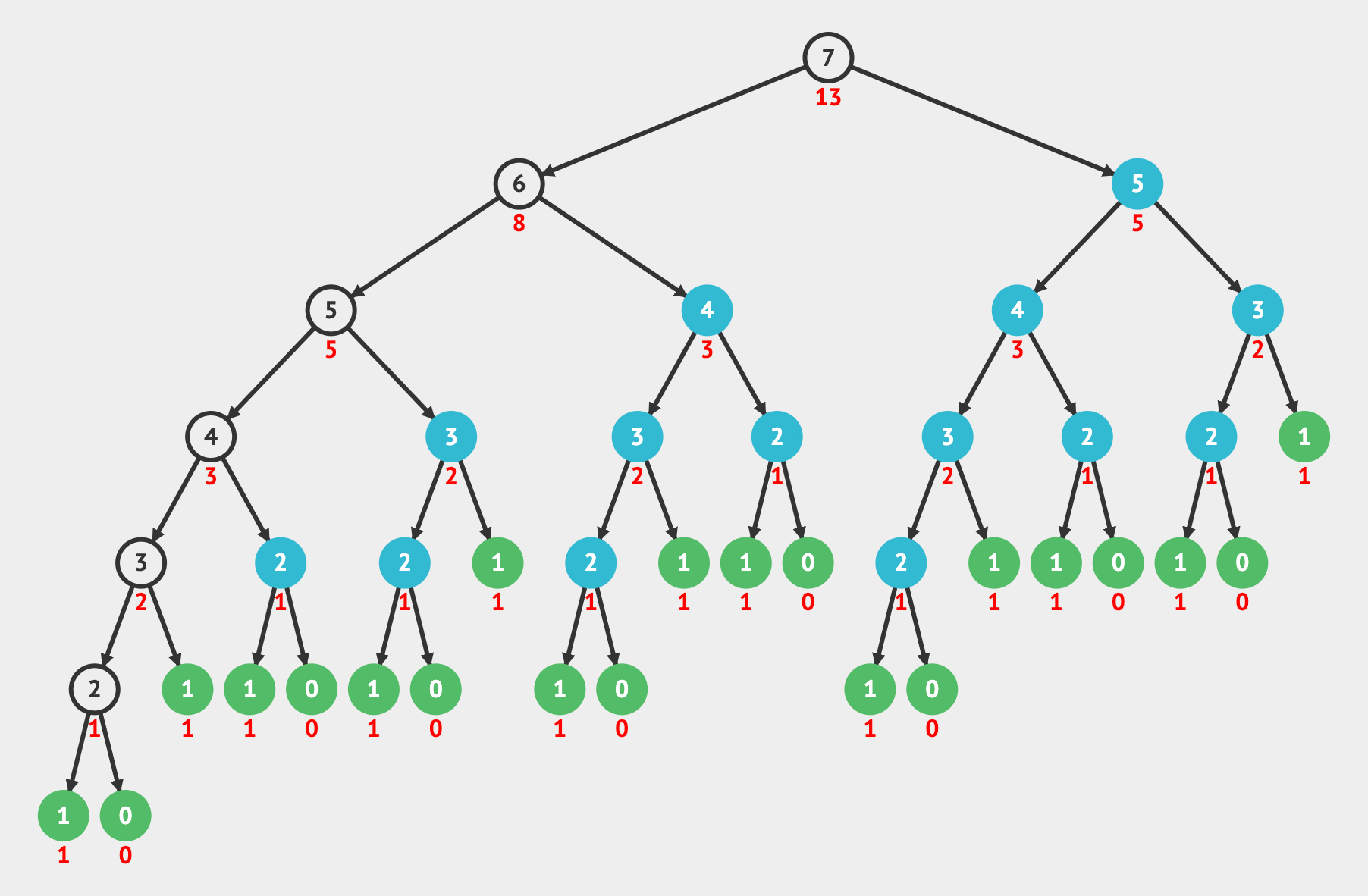
The items highlighted in blue are repetitive functions calls that use the same input multiple times. These are the overlapping subproblems. When visualizing the recursive calls as a tree, the branching is a sign that we'll have subproblems that overlap.
On the other hand, when calculating the factorial, we have subproblems, but we don't have overlapping subproblems.
Every time we call factorial, we pass it a new value that we haven't calculated the subproblem answer for.
So instead of creating a tree structure with branching, it simply forms a straight line.
When we have overlapping subproblems like in the Fibonacci example, this is when we are able to use dynamic programming. With dynamic programming, we utilize memoization to store the results of these repeated steps so that we only solve each overlapping subproblem once.