Memoization
Memoization (a form of caching) is an optimization that stores the result from a function call or expensive calculation so that the code isn't executed more than once for the same input. Like many of our optimizations, we incur additional space to improve our time complexity.
Memoization can be applied broadly in software engineering, but in interviews, we most often see it with dynamic programming for storing the results of subproblems.
Simple Example
For functions, we always expect them to return the same result when called with the same input. With memoization, we store the result of a function call for a given input so that we can return immediately instead of recalculating the answer.
The below example is contrived but still valuable to gain the insight.
Before memoizing, this function takes O(n) time because we go from 0 to n every time we call the function.
After we introduce memoization, it only takes O(n) the first time we calculate the solution for a given input n.
Then if we call the function again for any value of n we've already calculated, it will return immediately in O(1) time because we already know the solution.
Memoization and Dynamic Programming
In dynamic programming, we build up our solution by solving subproblems with different function input values and combine the results to get our solution. We use memoization to store the result for overlapping subproblems (problems called with the same input multiple times) so that we only have to perform the calculation once.
Calculating Fibonacci numbers is a classic example of using dynamic programming and applying memoization. Without memoization, it requires ~O(2n) time complexity.
Let's take a look at what is happening if we call fib(7) without memoization.
The number in the node is the input value for a recursive function call, and the tree represents how the recursive calls spawn additional calls.
We can see nodes containing the same input value appear many times which means they are overlapping subproblems trying to calculate the same solution.
Without memoization, we repeatedly solve for all the values each time.
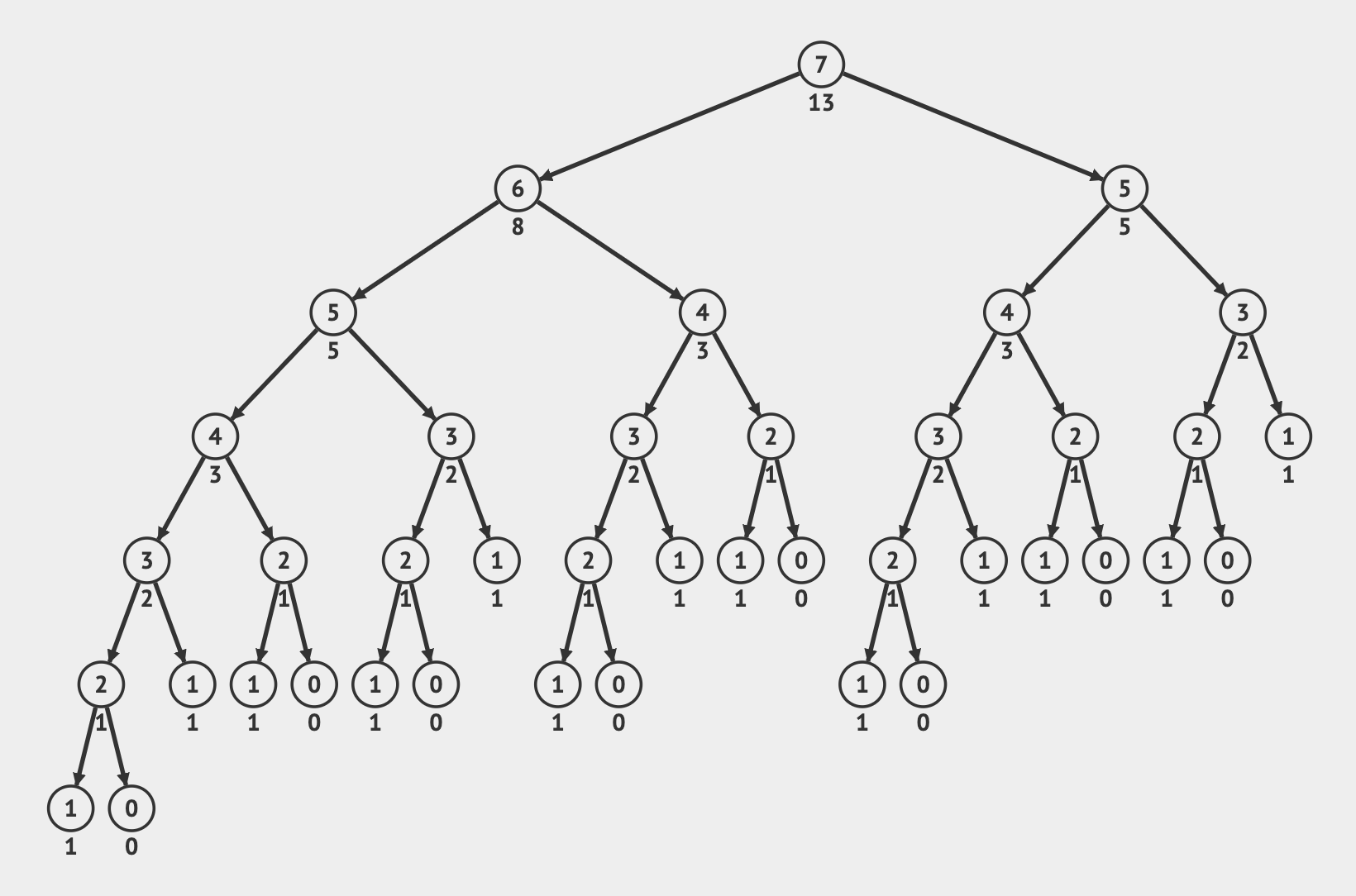
Not only do we call the same function many times, but each time it also triggers additional recursive calls. If we instead store the result of a function call, we can just use the memoized value that was previously calculated instead of going deeper into the recursive tree.
For this problem, we use a hash table where the key is the input value n for the fib(n) function, and the value for the key is the solution Fibonacci number calculated for that value of n.
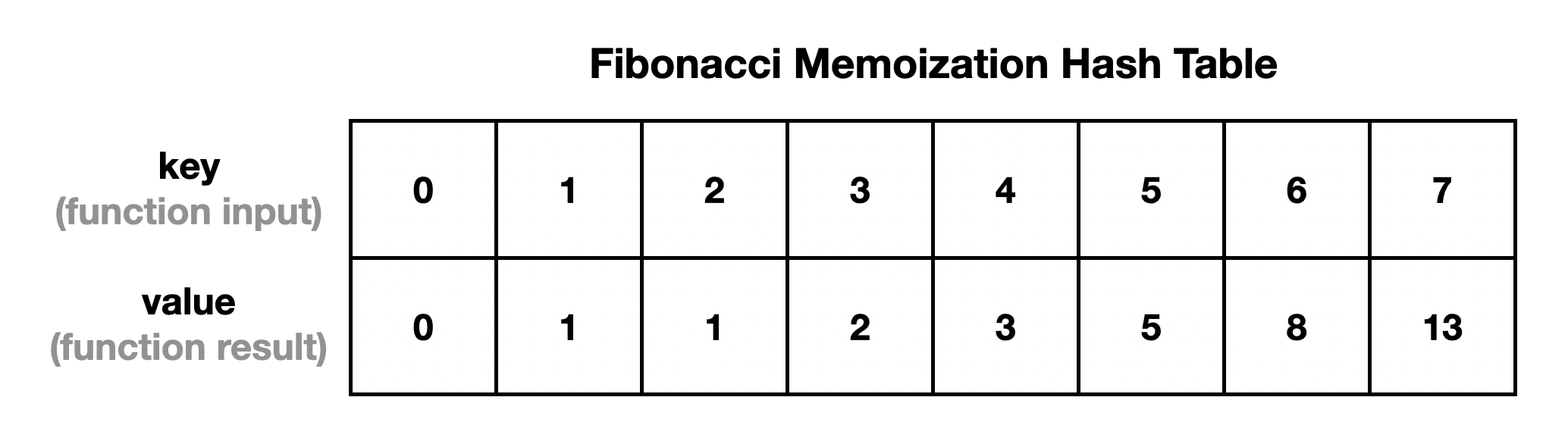
Which looks like:
Translating this to code, we get the following:
Now let's view our tree of recursive calls. The nodes highlighted in blue are when we have a memoized value and would return in constant O(1) time. The white nodes are the ones that calculate the result for that input for the first time. After calculating it for the first time, we store this result in the memoization data structure.
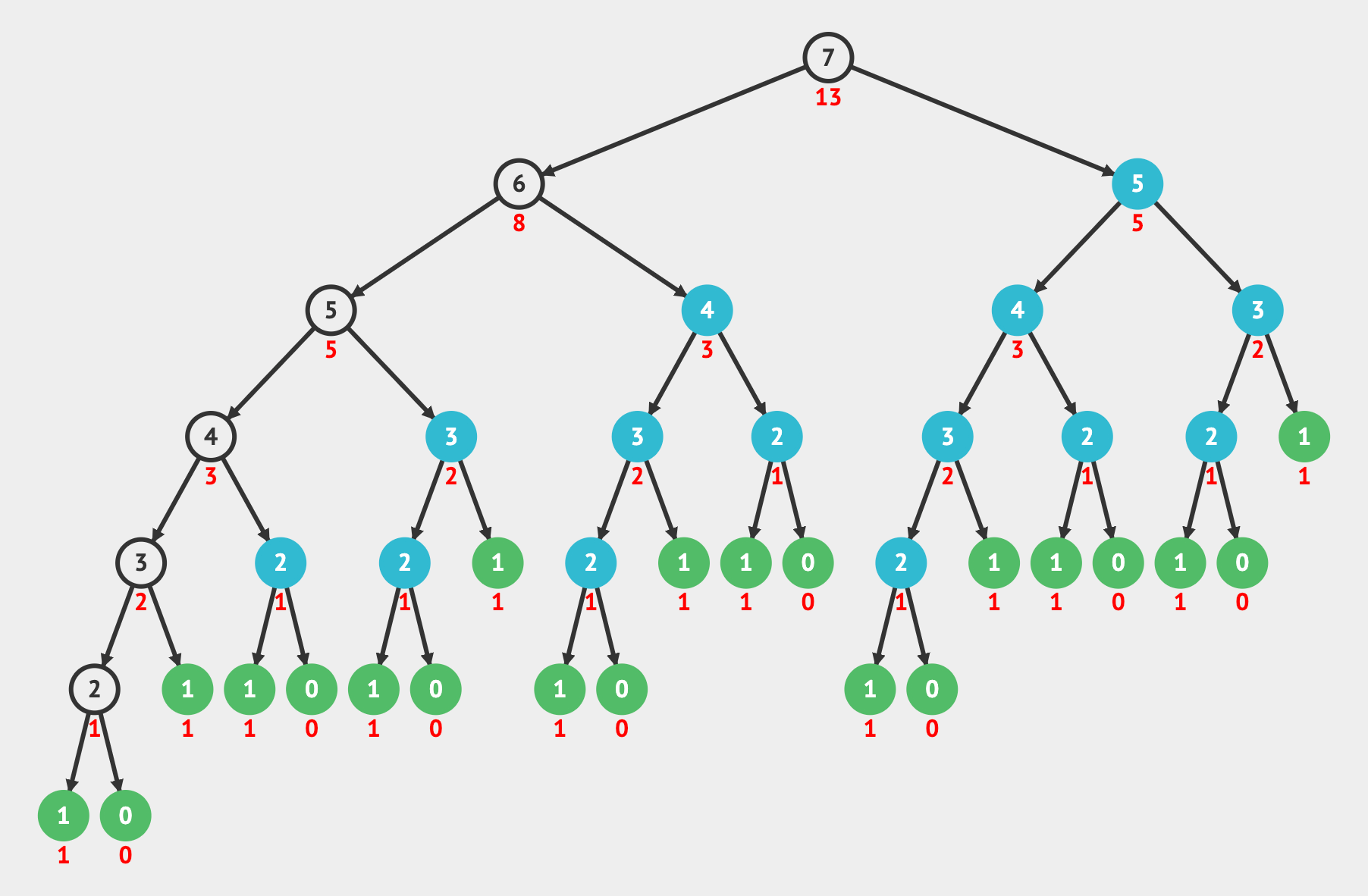
In fact, the first time we encounter a memoized value (blue node), we immediately return the result stored and do not continue executing the recursion. This eliminates many additional operations.
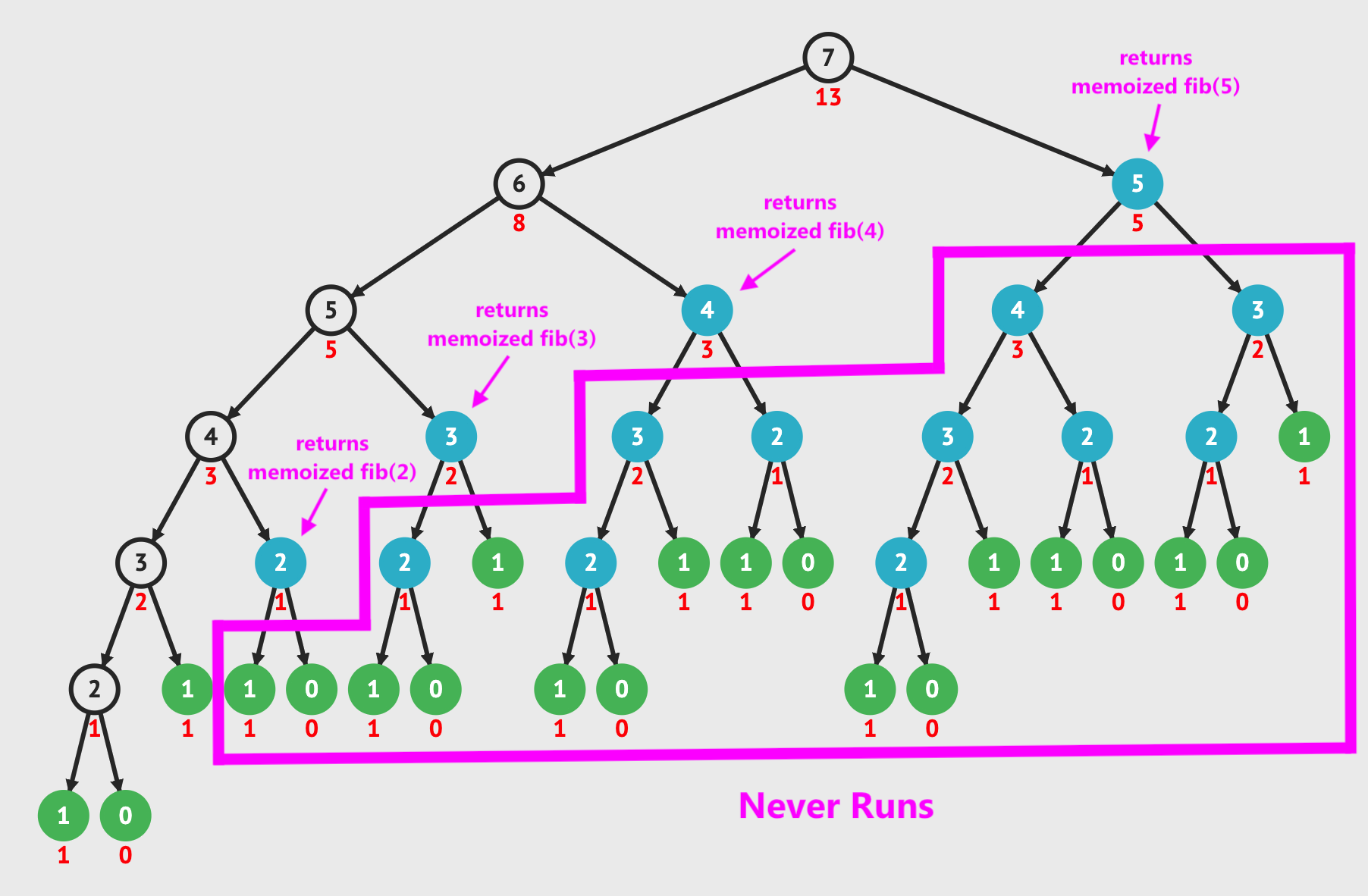
By using memoization, we improve our runtime from O(2n) to O(n).
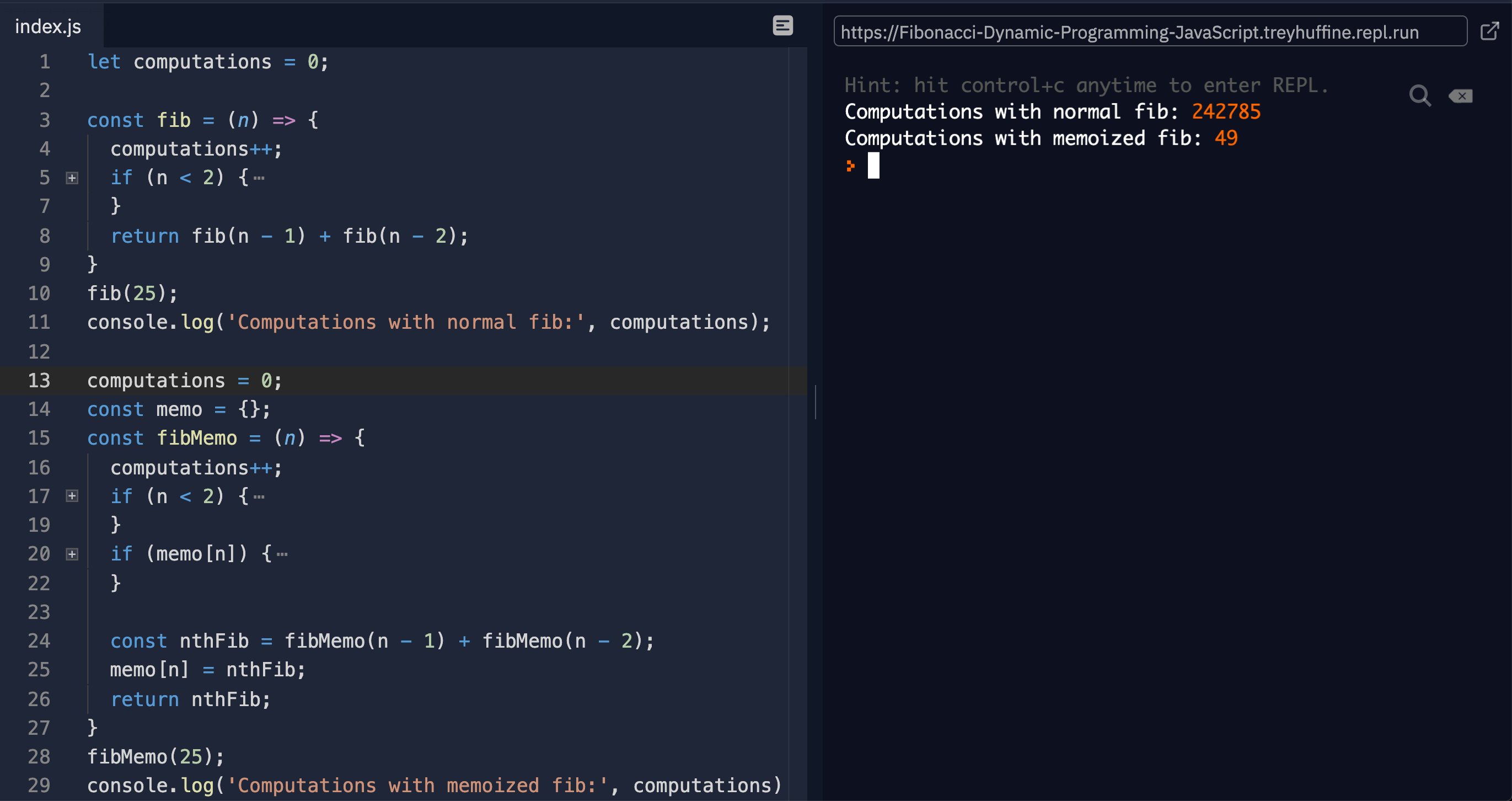
With an n of 7, this is 41 opertions versus 13, and as our input size increases, the difference grows dramatically.
If we increase the input size to n = 25, it takes 242,785 operations for the non-memoized version versus only 49 for the memoized version.
We can also memoize using a bottom-up approach. Again we use a hash table to store the intermediate values. Then we look backward in the hash table to use previous results to calculate the current Fibonacci number for each iteration of the loop.
Using a data structure is actually not required to calculate a solution for bottom-up Fibonacci since we can just store the previous two Fibonacci numbers in variables. However, very often in dynamic programming bottom-up solutions, you will need to construct a full table like this to solve your subproblems efficiently.
Memoization in Software Engineering
Not only do we see memoization in interviews, but memoization and caching are very common techniques used in production to keep our applications running fast. Anytime we calculate something "expensive" in our application, it is common to store this result instead of needing to recalculate it every time.
- The frontend uses memoization for UI state to prevent it from needing to re-render
- The backend stores expensive calculations in memory
- We cache frequent database queries in something like Redis to make the data immediately accessible