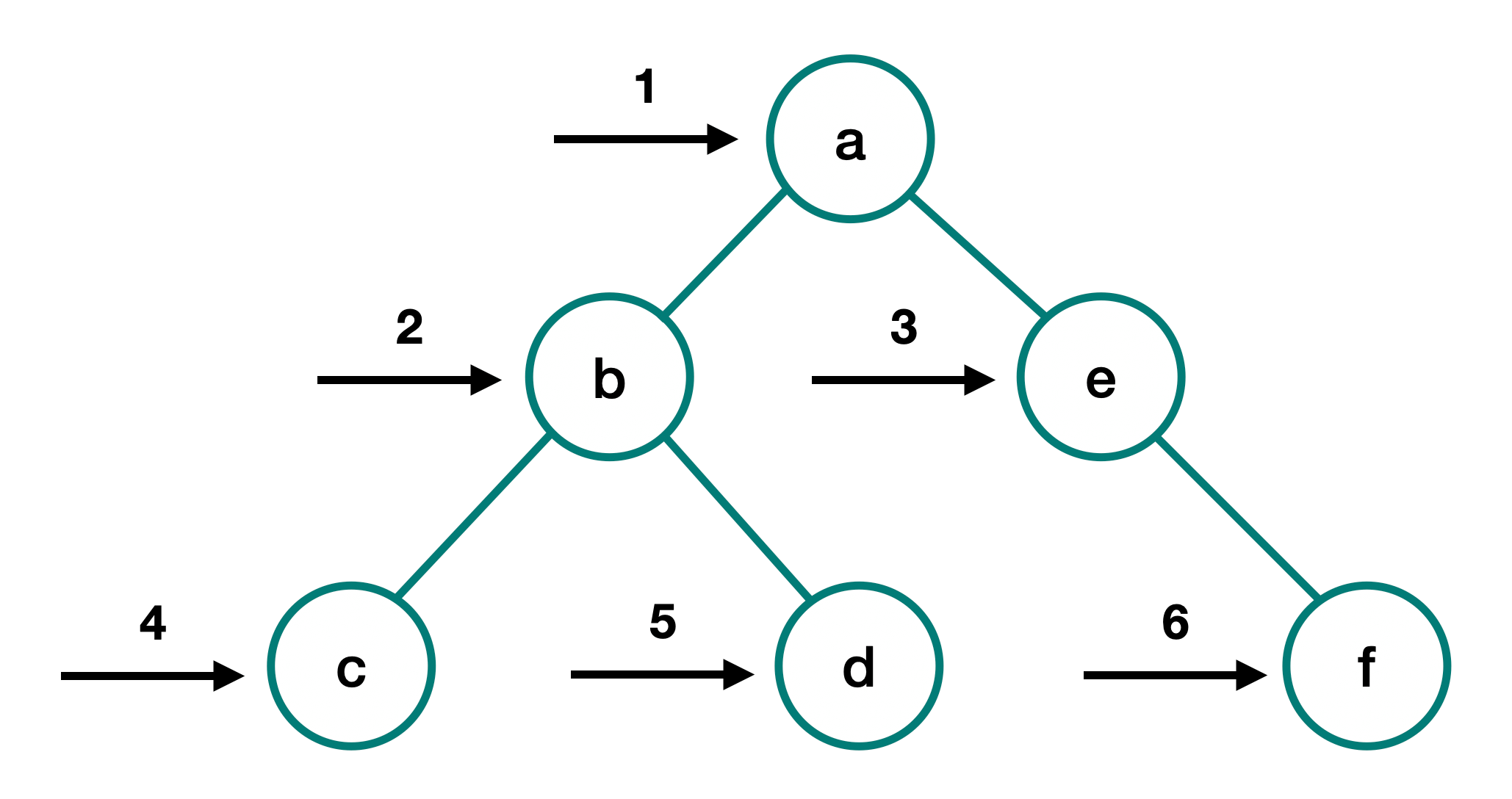
Tree Traversal: In-Order, Pre-Order, Post-Order

There are two methods to traverse trees: depth-first search (DFS) and breadth-first search (BFS).

DFS is the most common way, and it is performed by traversing to the leaf nodes. It goes as deep as it can and then moves on to the next branch. DFS is implemented using a stack or recursion.

BFS on the other hand traverse the tree by level and can also be called level-order traversal. So it will go all the way through level 1, then level 2, and follow this path until it reaches the last level. BFS is used to find the shortest path to a node.

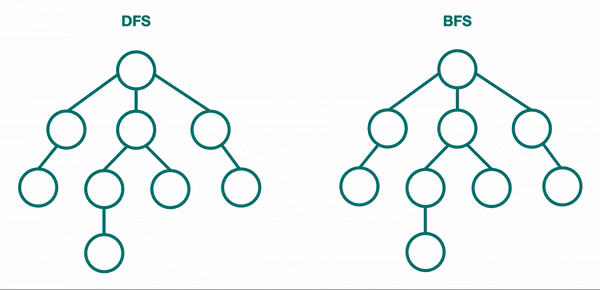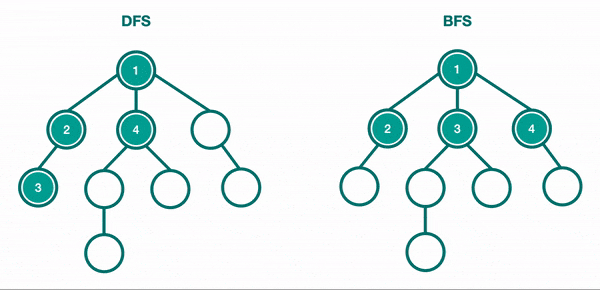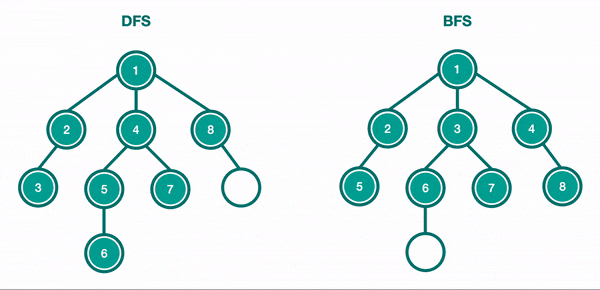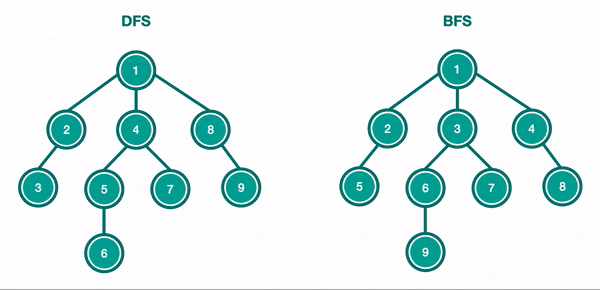
DFS is much more common with trees, so we will discuss how it's done here, and then discuss DFS vs. BFS in more depth in the graph data structure section.

There are three ways to traverse a tree using DFS: in-order traversal, pre-order traversal, and post-order traversal. Each of these implementations are DFS and explore down a path fully. The only difference is the order in which they use the current node's data.

In this article, we'll use the recursive solution to teach the concept because it is the best for gaining the initial intuition, and then in the interview questions, you'll get exposure to the iterative solutions as well.

Traversal Implementations

For all the cases, we will only consider a binary tree that has a left and right pointer.

You will notice that the code for each solution below looks very similar - almost identical. The only difference is when we "visit" a node which is when we use the current node's data in our algorithm.

Since we are using recursion, we are building up a stack of function calls, and it will unwind when we reach the leaf nodes which is the base case. What determines the order is if we "visit" the node before the recursive call, after visiting the left node recursively, or after visiting both the left and right nodes recursively.

The input function will be the following node implementation:

In our case we will consider visiting the node as just printing its data:

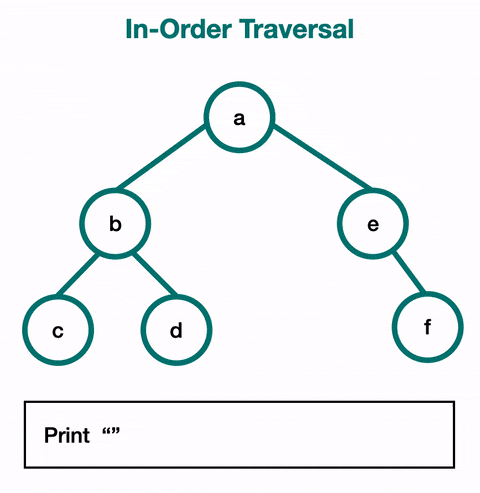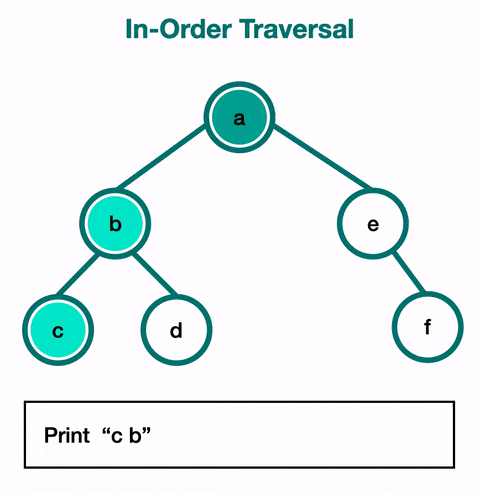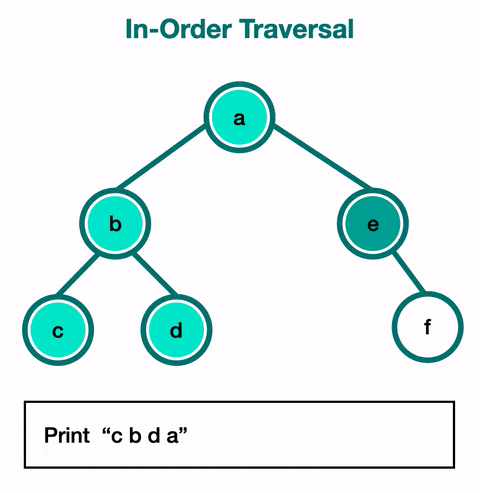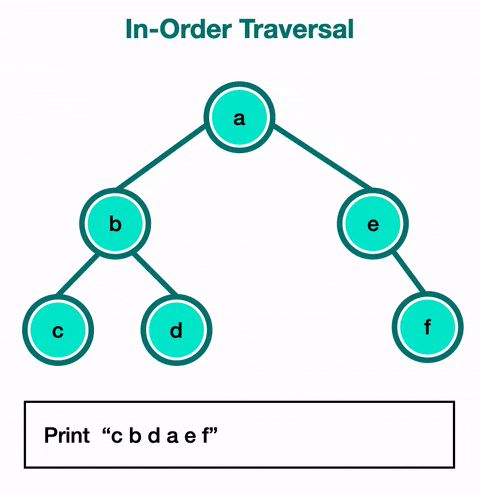
In-Order Traversal

In-order traversal is the most common and visits the nodes in ascending order. If it were a binary search tree, this will start with the smallest value at the left-most node and end at the largest value at the right-most node.

Use in-order traversal if you need to utilize the nodes as if they are in a sorted linear order.

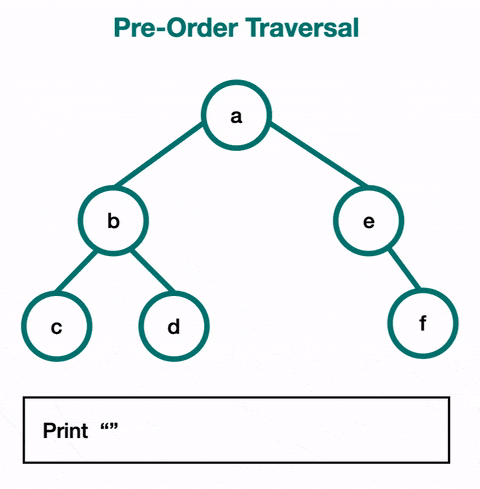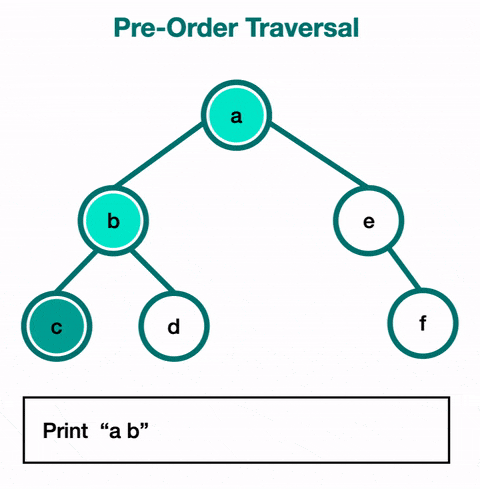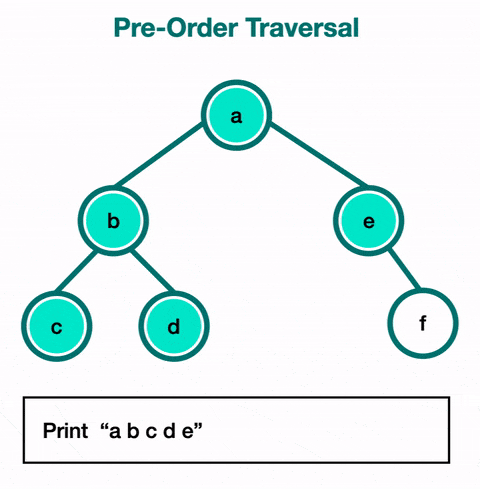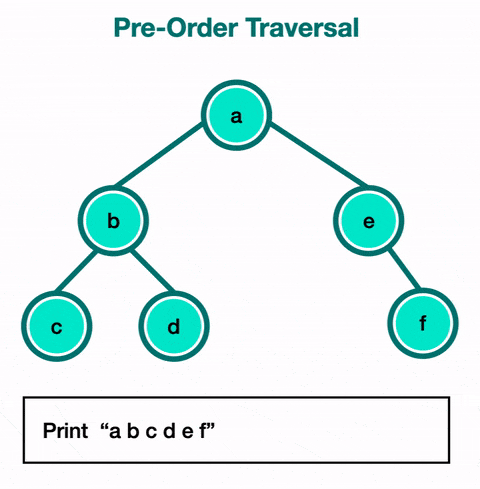
Pre-Order Traversal

Pre-order traversal will always visit the current node before visiting its children. The root is the first node visited. It follows the left path and visits each node as it encounters them. After that, it follows the right paths and still visits the nodes as it encounters them before continuing on with the path.

Use this if you want to explore a given level before reaching the leaf node of a path.

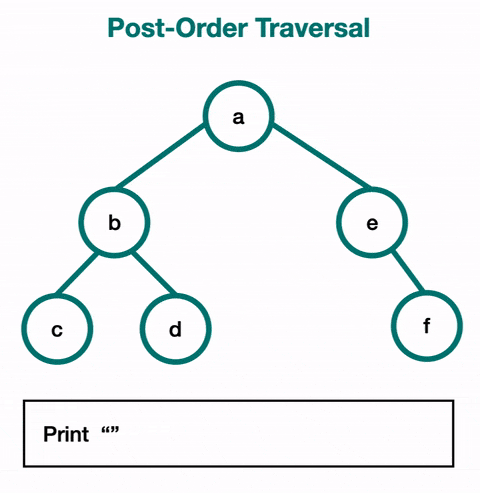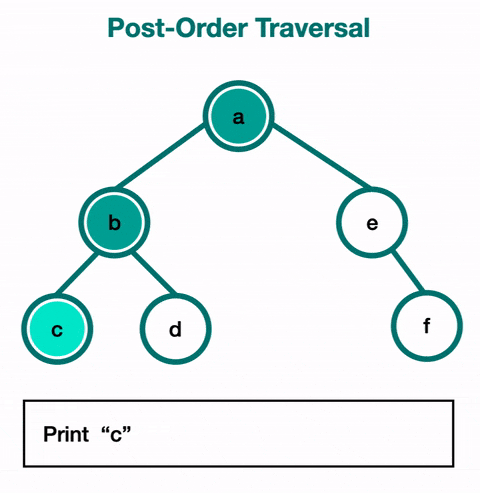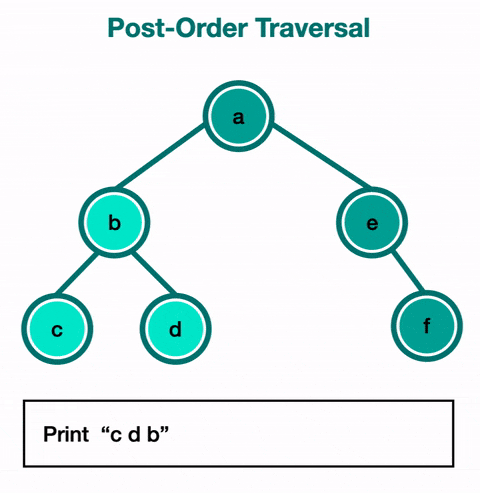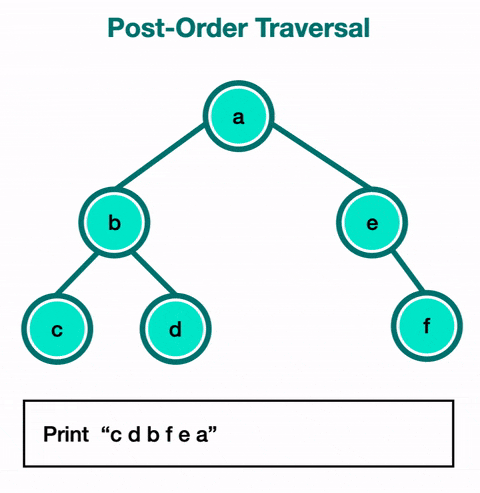
Post-Order Traversal

For post-order traversal, you visit a node's children before visiting that node. This means that you will use it when you want to reach the leaves first. You visit the entire left subtree, then the entire right subtree, and then the root node of the subtree.

Breadth-First Search

With breadth-first search (BFS) you use a queue data structure instead of a stack. It traverses across each level before going deeper into the graph.

We'll explore BFS further in the graph section as well.