Implement a Binary Search Tree

Building a binary search tree is an excellent exercise to understand how to navigate trees and feel comfortable using them in interviews. Our tree will contain an insert and search method. We will assume they can operate in O(log n) time, but we won't explicitly enforce this through balancing.

We will use a binary tree node that has the following implementation:

We will use a tree implementation which maintains our root node, and we will add the logic to insert and search for nodes.

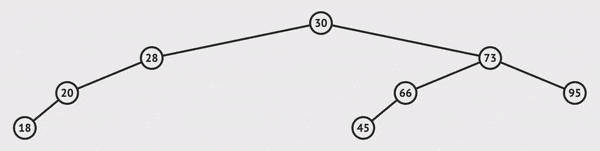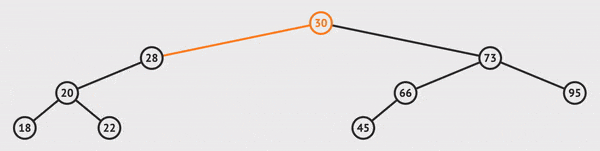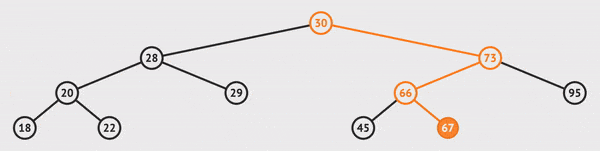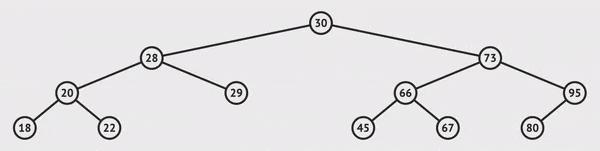
insert(data)

To insert a node, we'll call the method with the data that we want this item to hold. If it is the first node inserted (the root doesn't exist), then we set this value as the root.

If it's not the first node, we begin to traverse the tree to the left or right. If the data we want to insert is less than the current node, we go left. If the data we want to insert is greater than the current node, we go right. If we hit a null, we found the end of the path which is the location where this item should exist to be sorted correctly, and we insert the value there.

search(data)

This method will return a node if we find its value in the BST, or otherwise it returns null. We traverse through the left and right nodes by comparing the value we're looking for to the value of the current node.

Complete Binary Search Tree Implementation

Here is our complete binary search tree. You can also interact with the code in a REPL.