Breadth-First Search
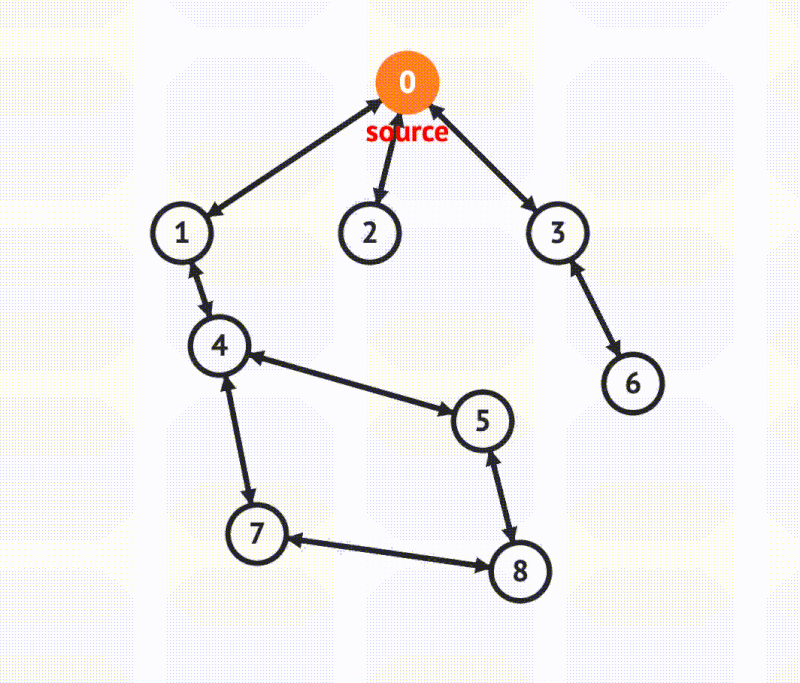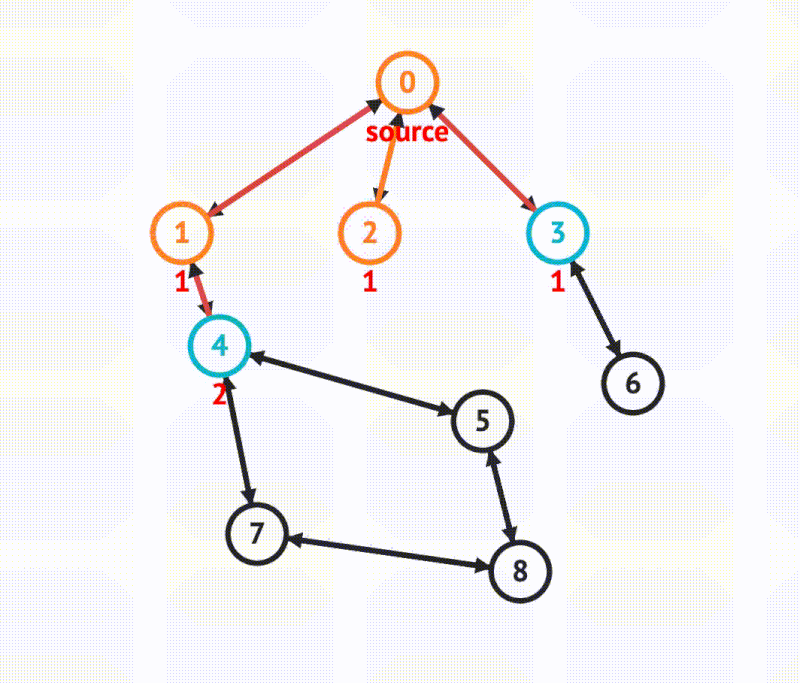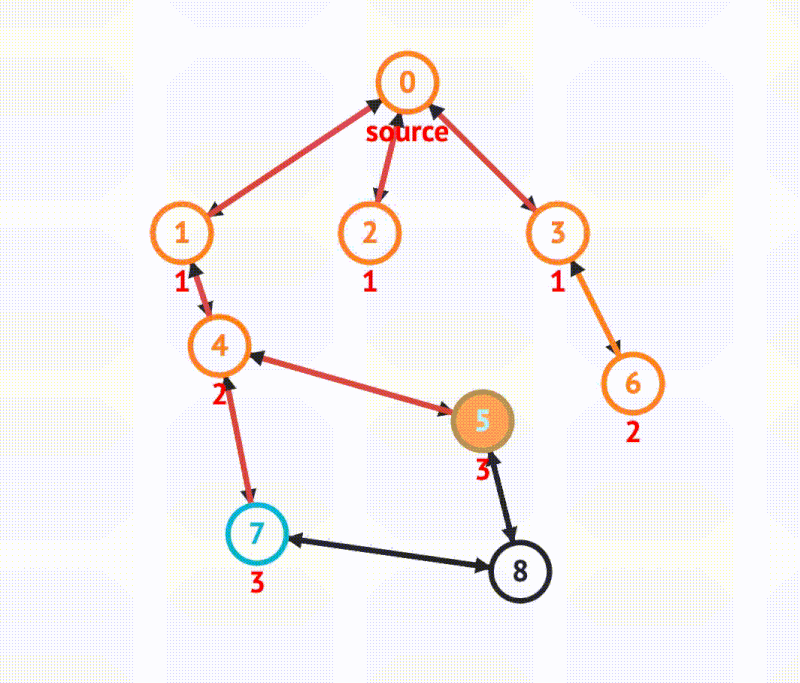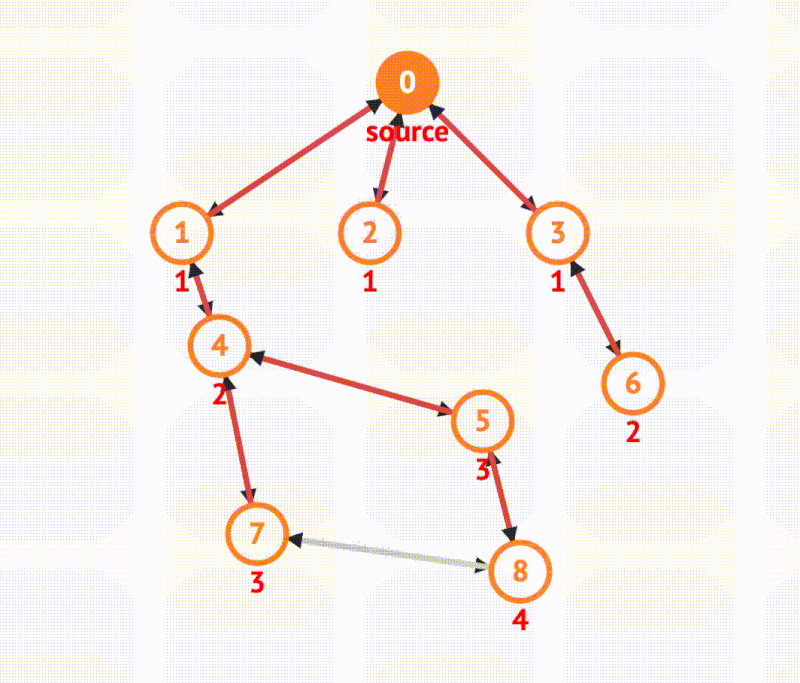
- Find the shortest pathIt considers all the nodes closest first
- More memoryBFS typically requires more memory (commonly assumed)
Breadth-first search (BFS) traverses by checking the nodes closest to a parent before moving on. BFS is used when we want to find the shortest path or closest neighbors.
Key concepts:
- Use a queue
- Go wide before deep (visit closest neighbors first)
- Track visited nodes to avoid cycles or multiple visits
- Find the shortest path to a node
I highly recommend watching the video to visualize BFS, understand why we use a queue, and gain a strong intuition with how it works.
BFS is implemented using a queue data structure. Because we access the items in FIFO order, we visit all the edges of a given node first and then progress onward.
BFS can be seen commonly in the real-world. For example, on Facebook we are recommended friends. What they do is create a graph of all the users and recommend the people closest to your friends since you are also more likely to be friends with them. The same thought process happens when Netflix recommends shows or Amazon recommends products - the closer the match is to you based on similar people, the more likely it's a fit.
To implement BFS, we will use a graph node that stores data and its edges.
The edges variable is just an array of pointers to its sibling nodes.
We will also assume our graph is undirected.
Nodes will take the following form:
We perform BFS iteratively by using a queue data structure. The full code can be found in this REPL.