BST Validate

Given the root node of a binary tree, write a function isBST that returns a boolean if the binary tree is also a valid binary search tree.

You can assume the tree won't be empty
The tree will not contain duplicate values

The nodes in the tree will be standard binary nodes:

Breakdown

Approach and test strategy

Inherited bounds for every descendant of a strict BST

Read the approach, boundary cases, and complexity

Carry the lower and upper bounds inherited from ancestors into each subtree. A node must satisfy both bounds before its children are considered. Comparing only immediate children misses a descendant that fits its parent but violates an older ancestor. This lesson uses a strict order, so an equal value also violates a bound.

Cases to check

Test a root alone and an unbalanced valid tree.
Put 12 below left child 5 of root 10: the local child relationship is valid but the whole tree is not.
Include duplicate values and values near the supported numeric limits without using them as accidental sentinel bounds.

Cost model

Visit each node once for O(n) time. Recursive auxiliary storage is O(h) for height h and can reach O(n) on a skewed tree.

Programming languages for this lesson

Starter code and reference implementations are available in:

The editor shows which of these languages can run on this deployment.

Follow teacher

Table of Contents

Validate My Answer

There are different iterative and recursive solutions that all have the same time and space complexity. Feel free to approach it in whichever way you feel most comfortable, and I'll provide both an iterative and recursive approach in my solution.
For a binary search tree, ALL the descendants to the left of a node are smaller, and ALL the descendants to the right of a node are larger. You must ensure that a node is not only correct for its immediate parent, but also all of the ancestors.
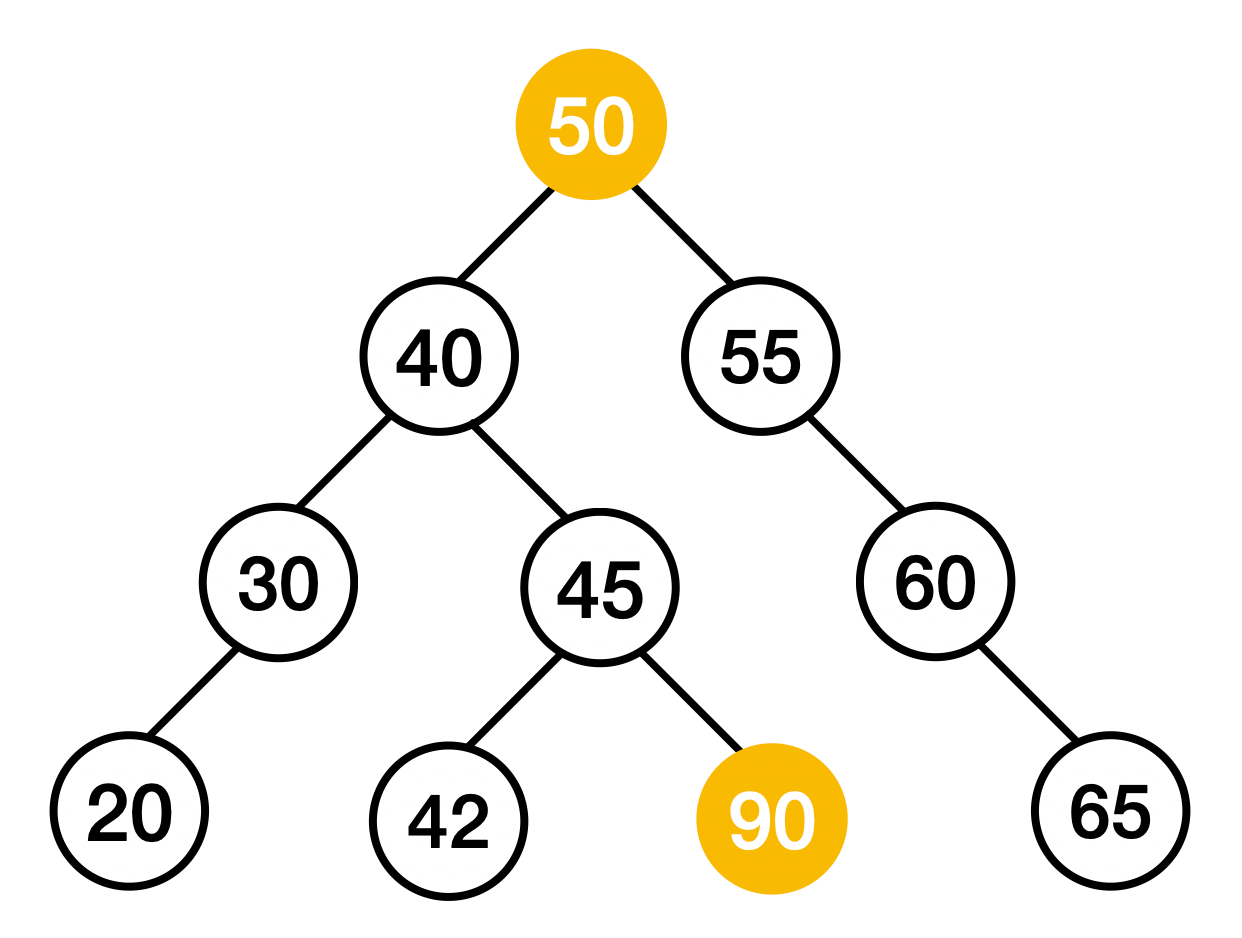
The worst-case Big O time and space solution in both the iterative and recursive case are O(n) where n is the number of nodes in the tree.

Follow teacher

Table of Contents

Test Results

Run your code and see results here...

/**
 * @param {BinaryNode} root
 * @return {bool}
 */
const isBST = (root) => {
  // Your solution here
}

BST Validate

Given the root node of a binary tree, write a function isBST that returns a boolean if the binary tree is also a valid binary search tree.

You can assume the tree won't be empty
The tree will not contain duplicate values

The nodes in the tree will be standard binary nodes:

/**
 * @param {BinaryNode} root
 * @return {bool}
 */
const isBST = (root) => {
  // Your solution here
}